2-损失函数和梯度下降

Author: haoransun
WeChat: SHR—97
图片&知识点来源：CS231N

1 损失函数

1.1 铰链函数

SVM常用损失函数是 铰链损失函数

如果预测猫，就将 猫这一列值和 cat 的分数作差，然后和0做比较，取最大值，求和。

汽车

青蛙

整个数据集上的损失函数

Python代码

权重的2倍，结果会是怎样？

奥拉姆剃刀原理：如无必要，勿增实体。因此选择数额小的。

1.2 正则化

L1 正则化 绝对值求和，L2正则化平方求和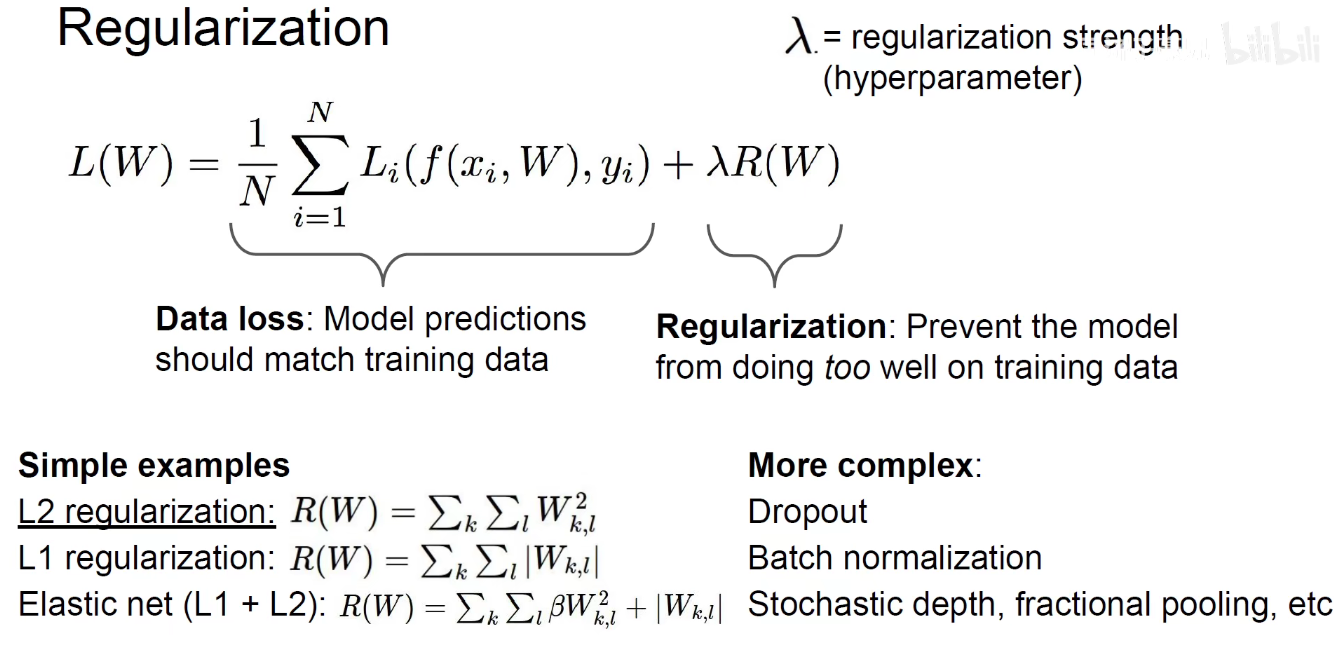

---

下面例子结果虽然都是1.

使用L1正则化是 1+0+0+0=1，0.25+0.25+0.25+0.25=1，不分伯仲。

而是用L2正则化，1 x 1 =1 ， 0.25 x 0.25 x 4 = 0.25, 更符合 “spread out” 权重的策略，雨露均沾。因此L2是建议选择权重w2.

---

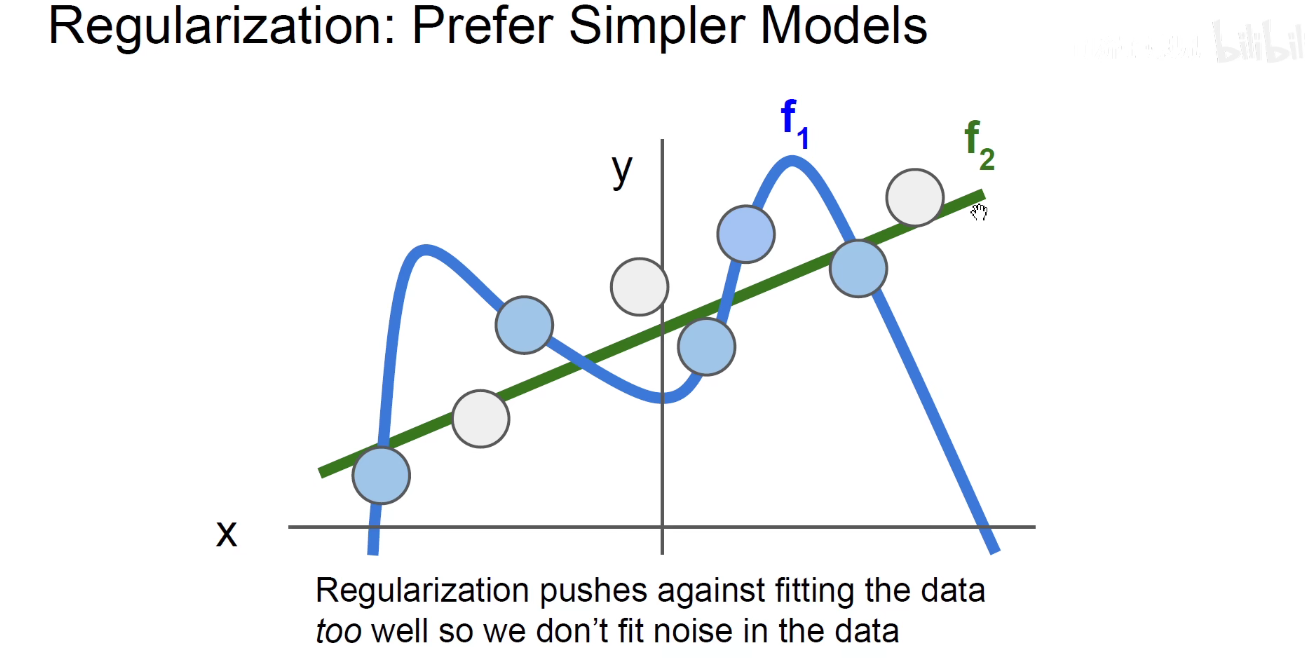
f1 过拟合，死记硬背了一些噪声点，模型搞得及其复杂，如果使用多项式函数来拟合这个模型，发现它的高次项系数非常大。

f2 大而化之的进行泛化，找到一个平滑的边界，没有去死记硬背哪些噪声点，y=kx+b

可以用正则化将f1高次项惩罚掉，就得到了一个简单的f2。

---

1.3 Softmax Classifier

如何将分数变为概率呢？概率都是0-1之间的数，且和为1。

首先对所有的分数都用e去进行次幂运算，如3.2 变成 e^3.2，e^5.1，e^-1.7，因为指数函数的函数值都是正的，且单调增加，所以可以把负数变成对应的正值，且对应单调性保留下来。

import math
math.exp(3.2)
math.exp(5.1)
math.exp(-1.7)

接下来用归一化，即

24.5/(24.5+164.0+0.18)=0.13

164.0/(24.5+164.0+0.18)=0.87

0.18/(24.5+164.0+0.18)=0.00

他们对应的大小关系被保留了下来，汽车的分数最高，概率中它的占比也最高。

softmax将分数变成了概率，即让他们的和为1，又保留了原始的大小关系，softmax本身不需要任何权重，只是进行了数学运算。后续所有的图像分类问题基本都是使用softmax作为最终的输出结果。

接下来需要构造一个新的损失函数，即交叉熵损失函数/对数似然损失函数/负对数似然损失函数/最大似然估计损失函数。 公式为：-log(正确类别对应的概率)

-log函数是过(1,0)点的函数，从天而降的函数，正确类别对应的概率越接近与1，对应的损失函数值越接近与0，（没什么损失），正确类别对应的概率越接近于0，对应的损失函数值越接近于 +无穷。只关心分类正确的概率，不关心分类错误的概率。

log(0.13x0.87x0.00)
刚才对猫 汽车 青蛙进行了分类，如果把这3张图片分类正确的概率进行相乘。就得到了使得这三张图片全部分类正确这一事件发生的联合概率。概率是0-1的，如果有1000张图片，就要将1000个0-1的数乘起来，得到的数非常小，为了解决这个问题。

我们可以使用对数来进行求解，对数可以将乘积化为求和操作。

log(0.13)+log(0.87)+log(0.00)，我们希望对数的值最大（对数也保留了单调性），log在0-1之间的值是负的，我们希望让这么多的负数加起来最大化，就在log前加一个负号，让加了负号的值最小化。

极大似然估计，就是求得所有图片都被正确分类的这一事件的联合概率。用对数将联合概率变为求和，又发现每一个对数的和是负数，为了让这一堆负数的和最大化，就在前面加个负号，让他们的值最小化。

熵：物理学中衡量混乱的程度

问题1：loss_L_i的最大最小值可以是多少？
最小值就是0，即正确分类是1的时候，最大值就是+无穷，即正确分类是0的时候。。

问题2：刚初始化时分数都是差不多的，这个时候交叉熵等于多少呢？
刚开始有C个分类，（此处为3），-log(1/c) = - (log(1)-log(c) ) = log(1) + log(c) = 0 +log(c) = log(c)，eg：log(10) 约等于 2.3。

1.4 Softmax VS SVM

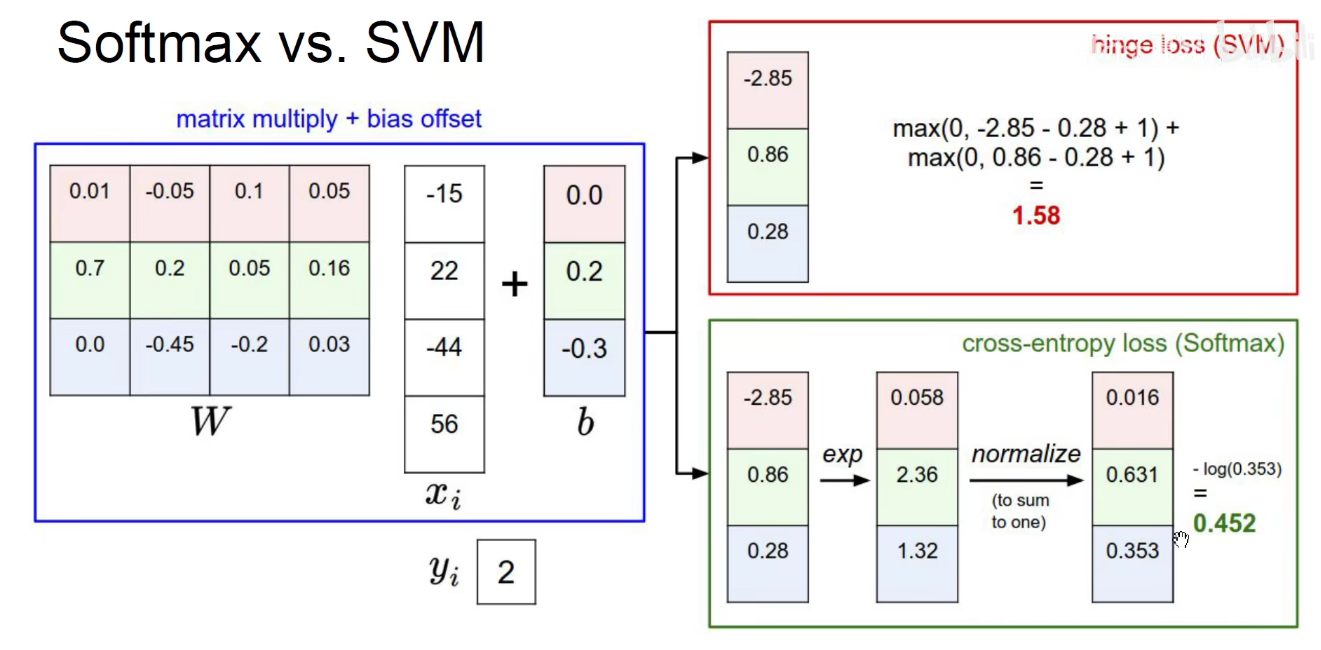
softmax尽可能将正确和错误的值分开，且值相差较大时，经过softmax变换会将值拉的更大。

1.5 损失函数回顾

2 Optimization

2.1 引导

让损失函数沿着山坡往下滚，能滚多低滚多低，最好滚到大海里，滚到海平面，甚至滚到地心里，这实际上是一个下山的过程。

策略1：随机选取

策略2：求导下山：找最陡的位置走，此处导数和梯度是一回事，derivative=gradient

导数求得是上山最快的方向，我们现在希望是下山，所以需要沿着反方向，在前面加一个负号。然后用它来更更新当前的权重，即求得损失函数对于每一个权重的导数，在前面加一个负号，加到之前的权重上，就可以按照反方向更新权重。

常用导数求导公式：

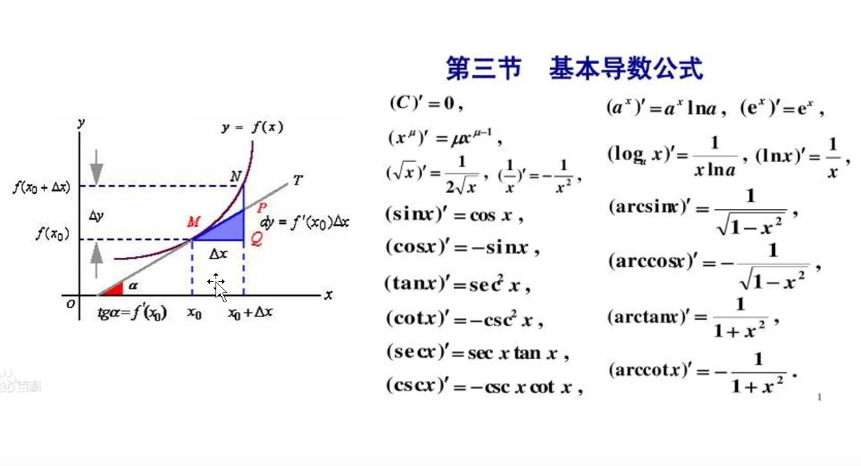
简单粗暴的方法求导数（取一个很小的增长数）：

(y-y0) / (x-x0) = k

上述方法是 数值梯度，比较慢，需要遍历所有维度上每一个值，且是近似求导。

用微积分的方法求得解析解（analytic gradient）

总结

2.2 Gradient Descent

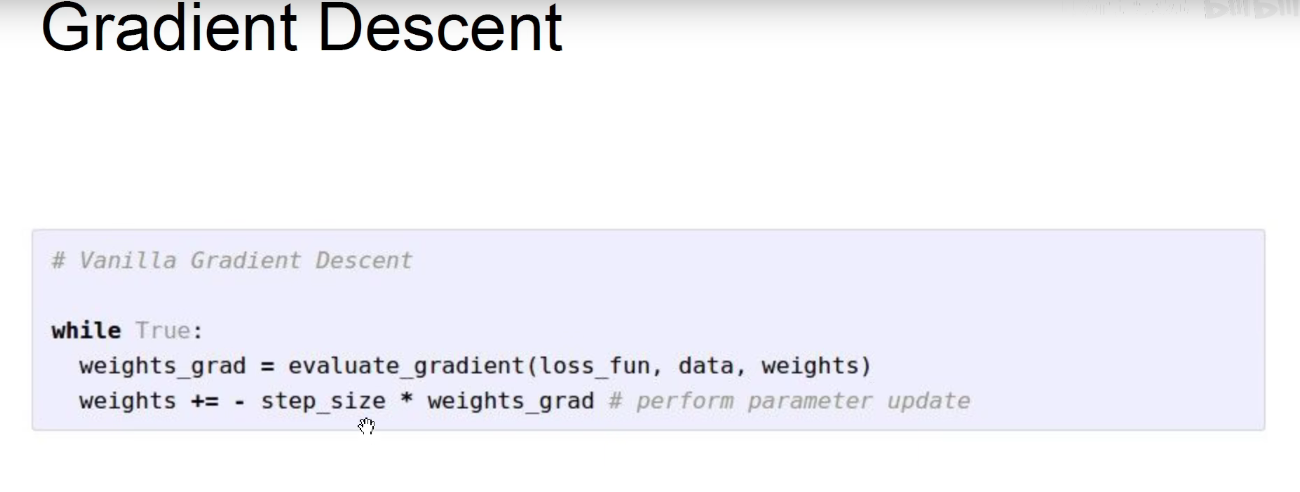
梯度下降：求得损失函数对于每一个权重的梯度，按照梯度的反方向乘以学习率去更新权重。梯度下降的下降指的是使得损失函数下降，而不是梯度本身下降。

step_size 表示学习率，是走小碎步下山还是大踏步下山：目的逼近最优解。

2.3 Stochastic Gradient Descent(SGD)

3 特征工程

选取合适的样本特征，是极为重要的一环。

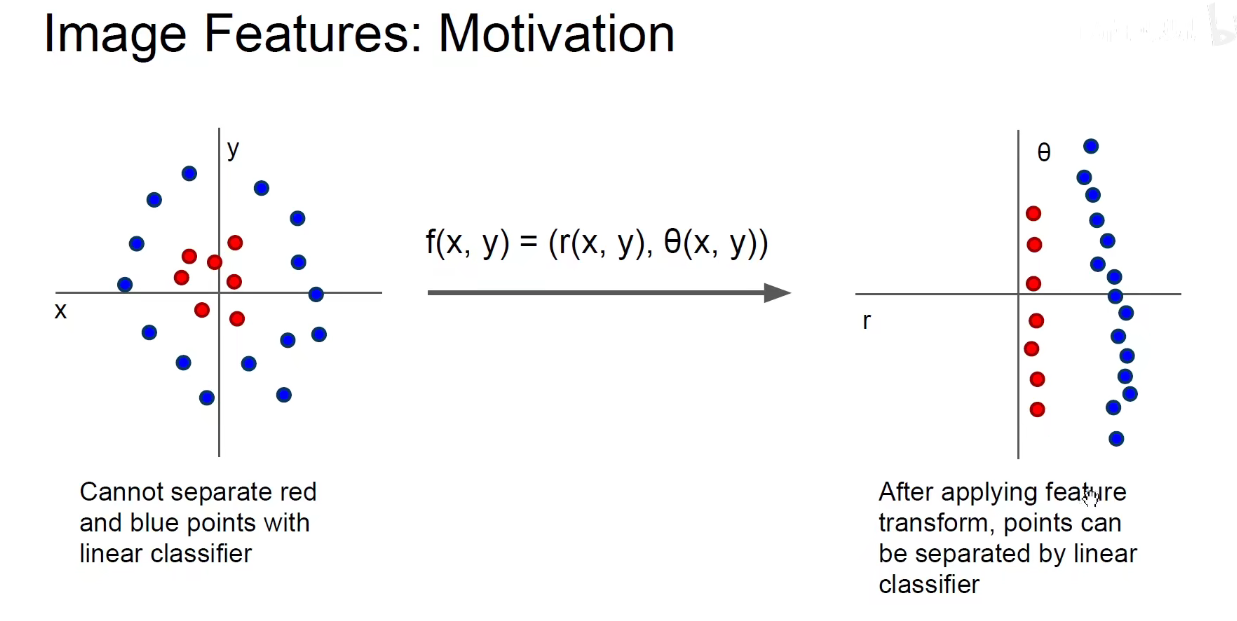
上述图片用线性分类器是分不开的，需要先进行特征工程，将坐标转换为极坐标，就可以被 linear-classifier有效分开。

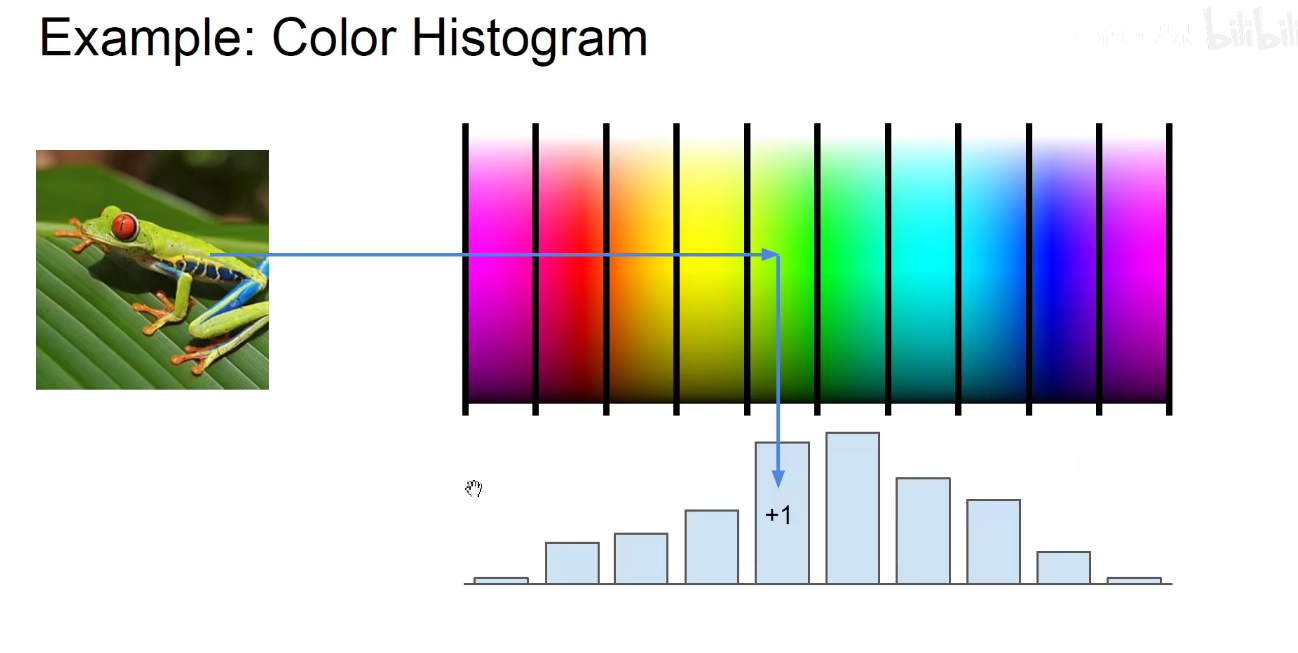
又比如 上图是将图片不同颜色通道的直方图提取出来作为特征。

或者上图 将 图片的 梯度方向直方图 作为特征。

上图是李飞飞读硕士时发的论文，将每一个图片拆解成多个小patch，用聚类的方法得到不同主题下的文本（像单词一样），当来了一张新图片时，将它对应的patch找出来，就如同找出来单词一样，再到原来的单词库中进行比对，看哪个出现的最高，就大概猜测它属于那个动物分类。

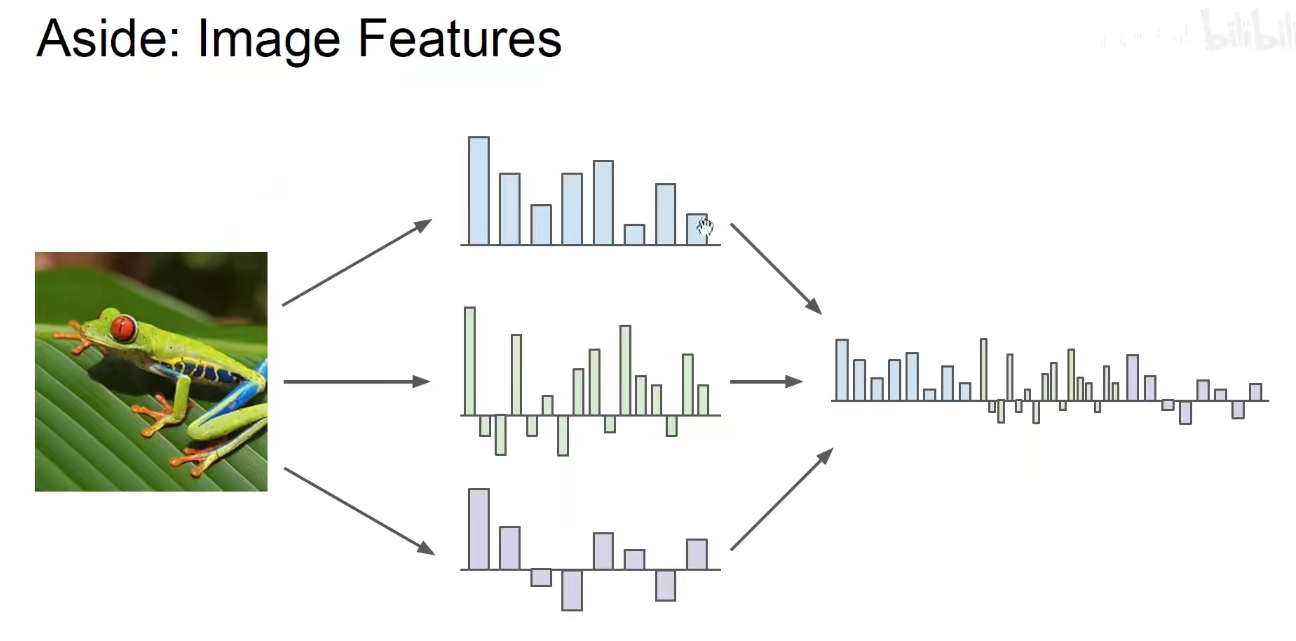
上述就是抽取不同特征作为组合特征。