Author: haoransun
WeChat: SHR—97
图片&知识点来源:CS231N
1 回顾
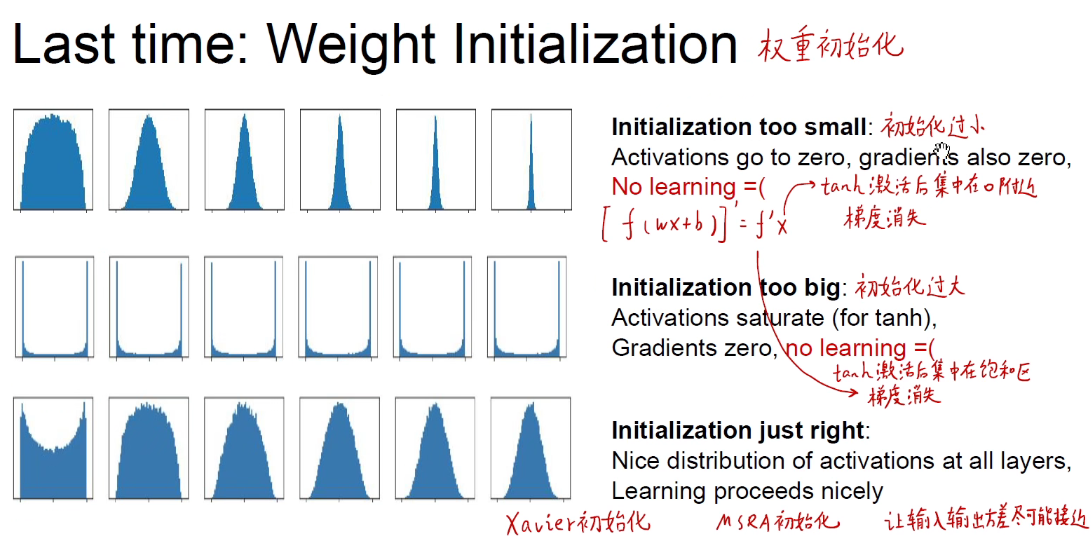
Xavier初始化: w 和 x 都关于0对称,且独立同分布 iid。
MSRA初始化: 何凯明团队专门针对ReLU函数做的。不需要上面关于w和x的条件。
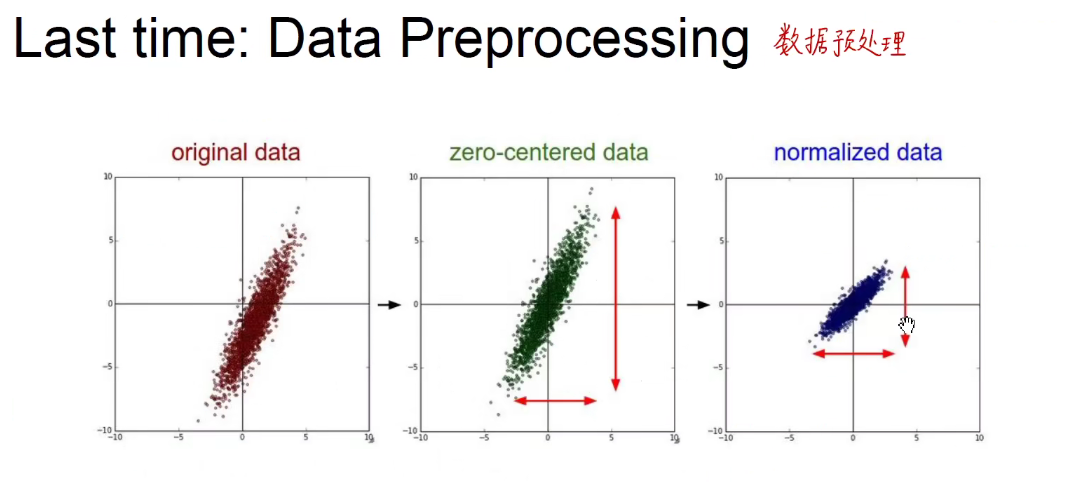

批标准化可以大大的防止过拟合,大大的加快收敛速度,并且起到正则化的效果。

2 Optimization



优化器:找到不同的下山策略。
之前学习的是前向传播求损失函数。反向传播求损失函数针对每一个权重的梯度。即找到每一个权重它下山最快的方向,然后按照下山最快的方向去迈一个学习率的小碎步,这样来进行更新和优化,通过不停的迭代来更新权重。
2.1 SGD缺点

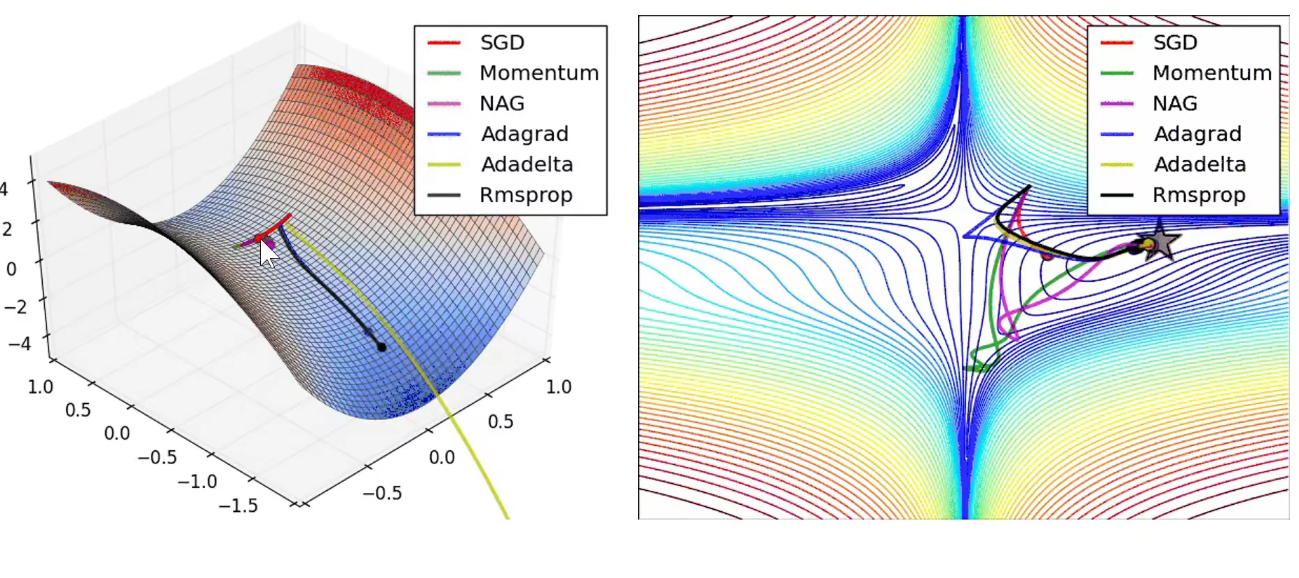
如上图所示:是一个等高线,是一个二维的输入。我们希望最终能够优化到笑脸这个地方。
现在随机初始化的地区是图中红色球,对它求导数会发现它下山最快的方向是图中的优化方向,即斜线。可以分解为水平方向(梯度小)和垂直方向(梯度大)。
我们希望他能够沿水平方向更新的多一些,但是按照图中的方向,是竖直方向更新的更大一些,即真正优化的方向没有优化多少,反而在不应该优化的方向优化的太大了。 第一步就会如下图所示,迈到尖角处(竖直方向的优化力度很大),即山谷的另外一边,再次求偏导数,又是在竖直方向优化力度大,又迈了回来,山谷的这一边。

如上图所示:就会在梯度较大的方向上产生振荡,可以用更小的学习率去解决,即每次都不让它迈那么多,只迈一丢丢,不迈到山谷的另一边,但是随着学习率的减小,我们真正应该更新的方向即水平方向迈的步子就更小了。
所以,不能简单通过减小学习率来解决振荡问题。这样会过犹不及。
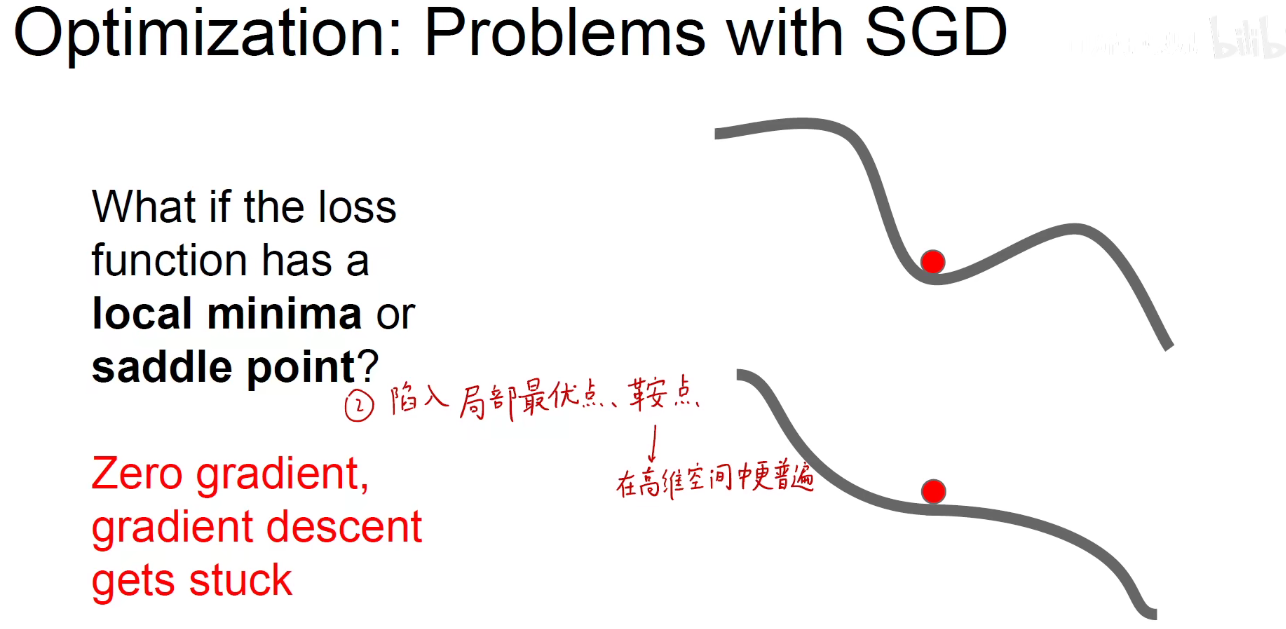
局部最优点:并不是全局的最优点,只是一个小盆地,一旦陷入,朝各个方向都找不到突破口。
鞍点:梯度为0,虽然没有被陷入到一个局部最优点中,即盆地中,但我举目四望,周围的梯度都是0,鞍点在高维空间中更加普遍。对一些权重来说,是开口向上梯度为0的点,对另一些权重来说,是开口向下梯度为0的点,开口向上与开口向下一交,像马鞍一样,就是鞍点。
如下左图,从侧边看是一个开口向下的,从正面看是一个开口向上的,就是一个马鞍。
2.2 SGD
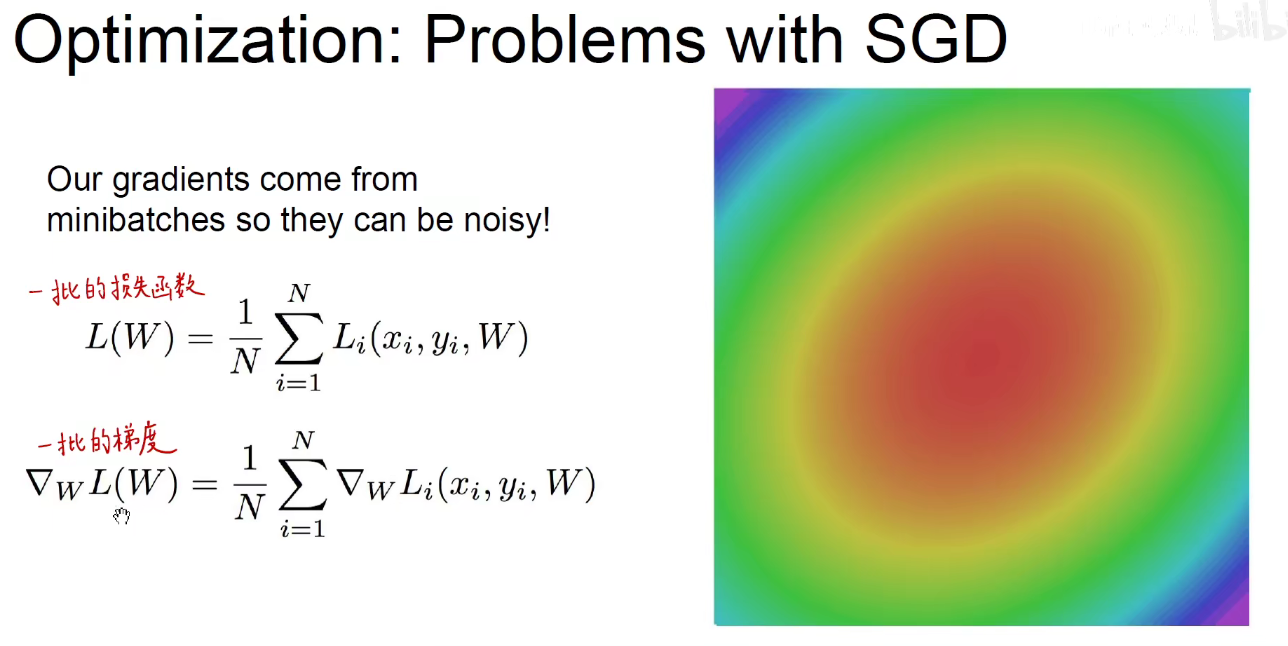
如上图:求得一批损失函数,求这一批损失函数对于每一个权重的梯度,即求得一批梯度。

如上图:现在来考虑如何让他下山的更快更好
之前(左边)是一步一步的下山,走走停停,每一步迈出后,看当前位置哪一个方向下山最快。这是很不明智的,因为走一步,看一步,得过且过,活在当下,是没有远见的。
如果我是一个大胖子,具有一个惯性和动量,我从山坡上冲下来,我从珠穆拉玛峰冲到四川盆地,就算人到了四川盆地,我想停下来,可人是个大胖子,我停不住,借着这股冲劲儿和惯性,就能够冲过四川盆地右边的山脉,到达武汉平原。这个思路就是动量。即右图。

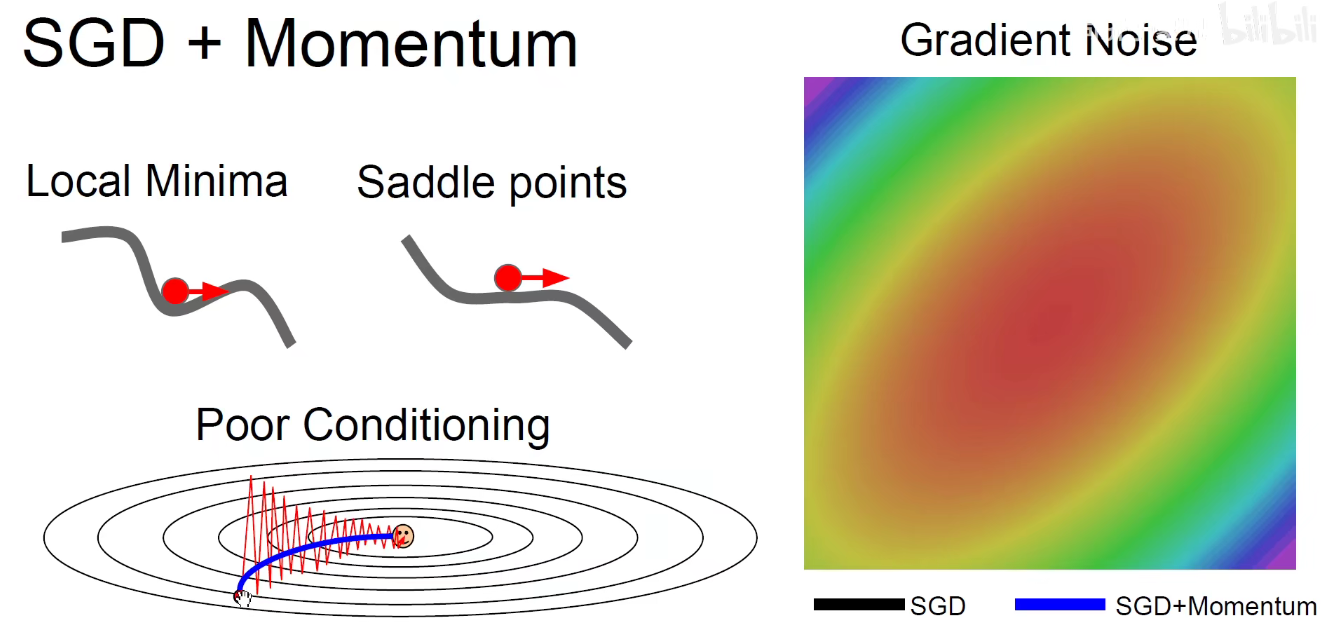
如上图所示:每次振荡都是相反的,每次加上dx,就抵消了。所以动量起到了一个平均平滑的作用。在该更新的方向上进行更新。而不是像之前单纯的SGD,走一步看一步,充满噪音和振荡。


带动量的绿色球由于动量总要偏离方向,再慢慢收敛回来,凭空增加了训练时间。
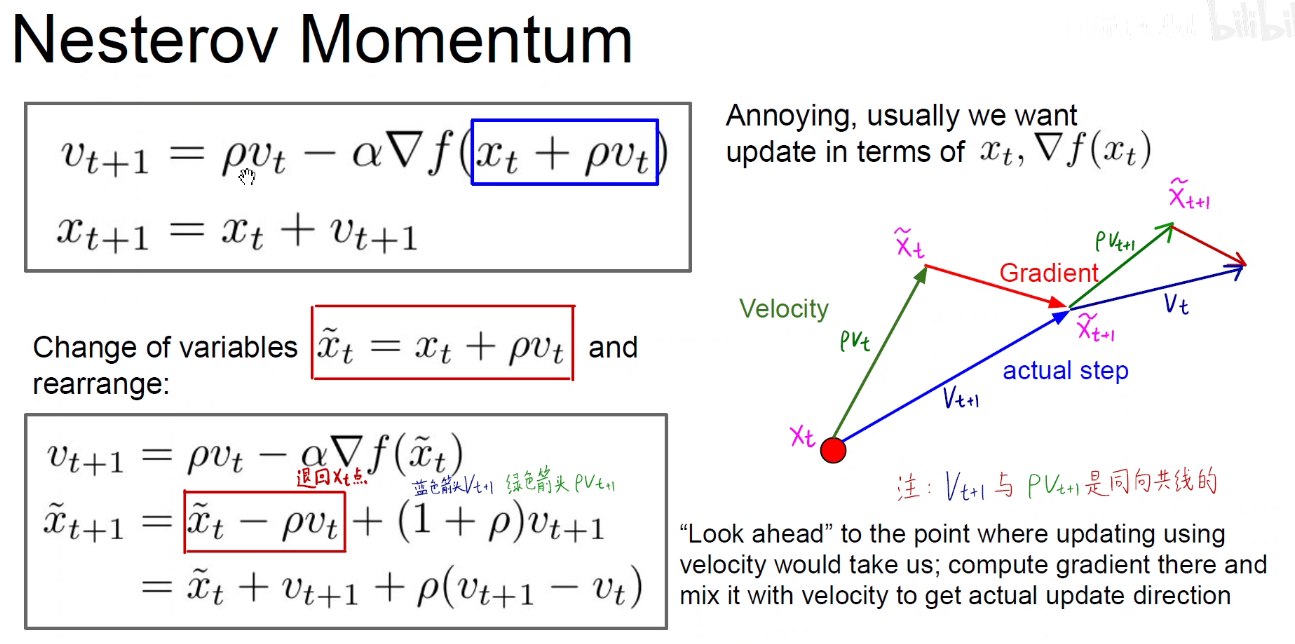
2.3 动量优化-Nesterov
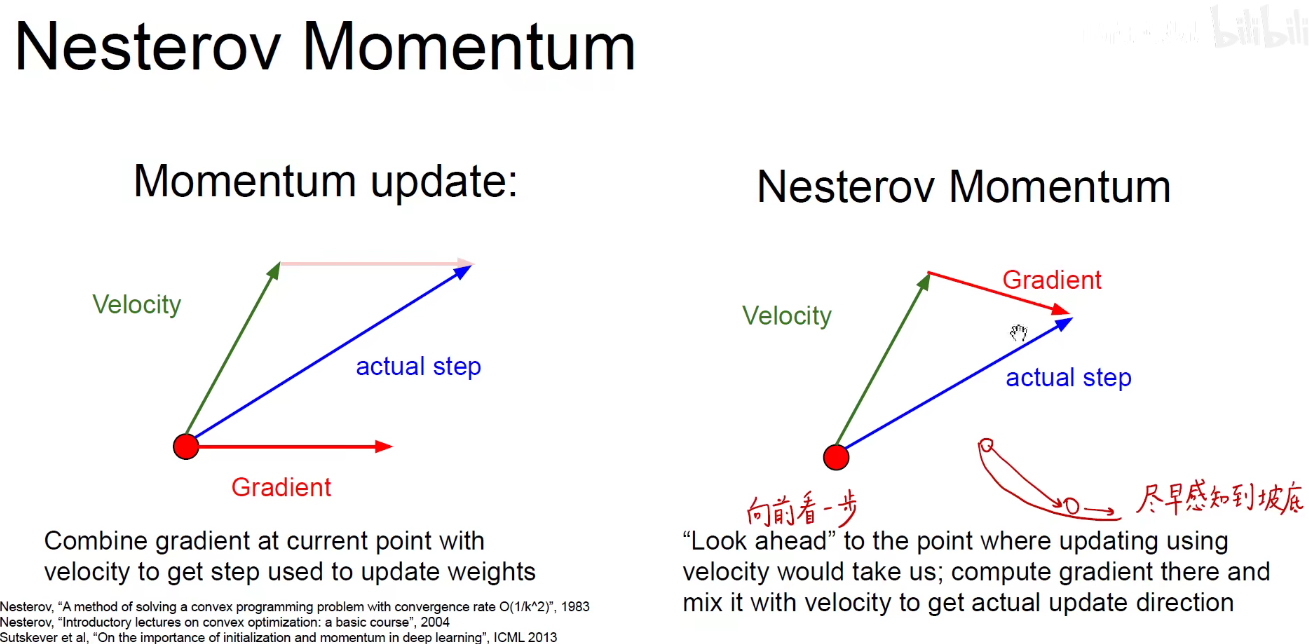
动量原理如上述左图:绿色是之前的速度方向,红色是当前位置的梯度方向,对这两个向量做一个矢量和,用平行四边形或者三角形法则,就得到了当前真实的优化方向。
右图是对动量的优化改进-Nesterov Momentum:既然按照现在速度的方向进行更新,那为什么求当前点梯度的方向呢?按照当前速度更新的某个点的梯度方向(即左图中粉红色实线,右图中红色实线)和原来的速度方向(绿色)做矢量和,这样就往前看了一步,好比下象棋,棋高一着,提前考虑一步,这样就能更早的使动量提前得到优化。
尽早感知到坡底,防止大胖子冲的过头了。还得调整回来。

2.4 动量优化-AdaGrad
既然SGD的弊端是在梯度较大的方向上发生了振荡,直接给梯度较大的方向加一个惩罚项,dx x dx,把历史上所有的dx x dx求和起来,让更新的方向除以惩罚项,(如果梯度很大,dx很大,那么分母就会很大),进一步更新的量就会变小。

AdaGrad就是对梯度大的方向加一个惩罚项,并且惩罚项是越来越大的,避免它在梯度较大的方向上发生振荡。问题:惩罚项越来越大,分母就越来越大,更新量越来越小,最后甚至不会得到更新。


衰减至0
2.5 动量优化-RMSProp: Leaky AdaGrad

decay_rate:我们要保留多少之前的grad_squared惩罚项。
如果 decay_rate = 0 ,表示我们不考虑之前的惩罚项,只考虑当前的dx x dx
如果 decay_rate = 1,那更新项就变为0.
2.6 Adam(almost)
AdaGrad是对梯度较大的方向进行惩罚,动量是对之前的一阶梯度进行求和累积,将这两者结合,称为Adam算法。

训练技巧:刚开始时第一动量和第二动量都是0,他们需要经过较多轮的更新后才能够预热和就位,发挥作用,我们希望他们可以在一开始就发挥作用,可以对他们进行偏差处理,如下图所示:


3 Learning rate schedules
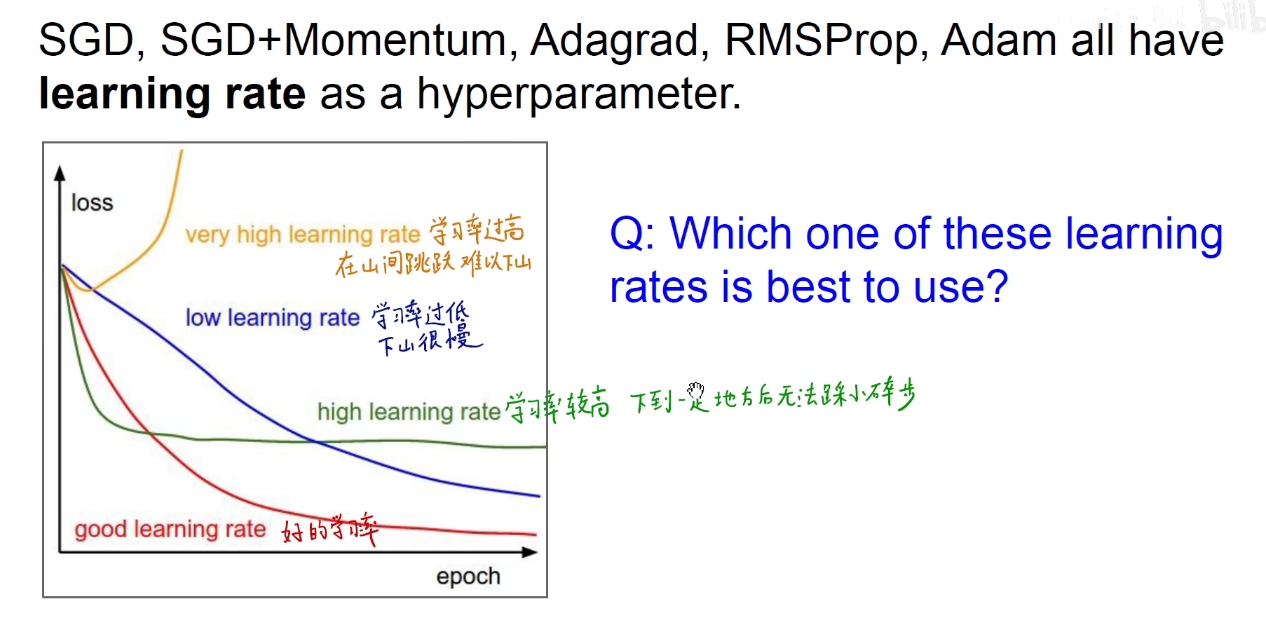
如上图:学习率过大导致在山顶跳跃,难以下山,学习率过低导致下山太慢,学习率较高,下到一定地方后无法踩小碎步下山。

可以如上图:训练初始采用大学习率,后期采用小学习率的动态调整策略。
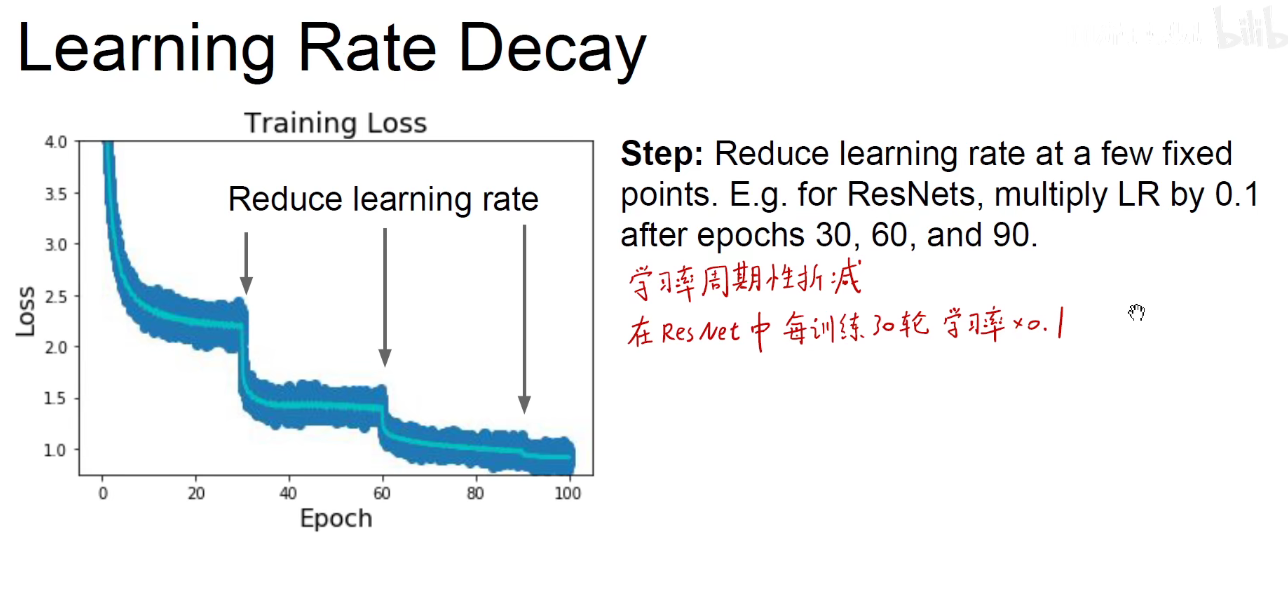
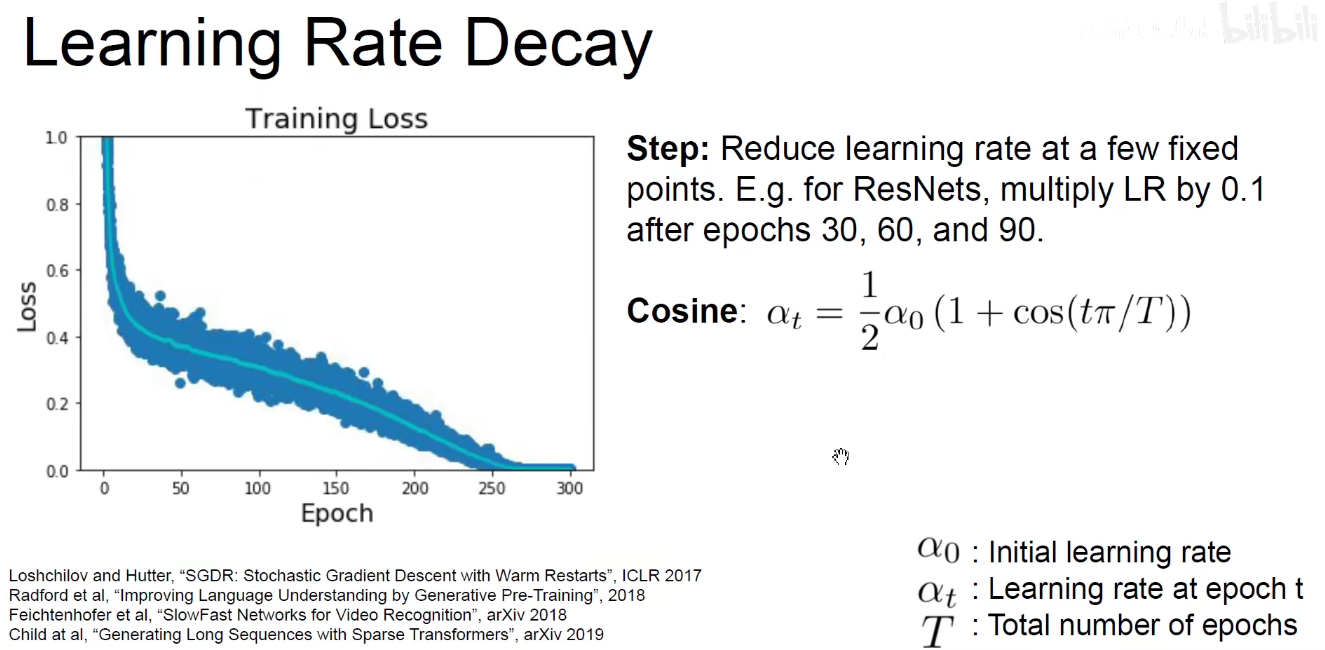
如上图:学习率周期折减,在ResNet中,每训练30轮,学习率乘以0.1
余弦形式减小学习率,训练轮次越多,学习率越小。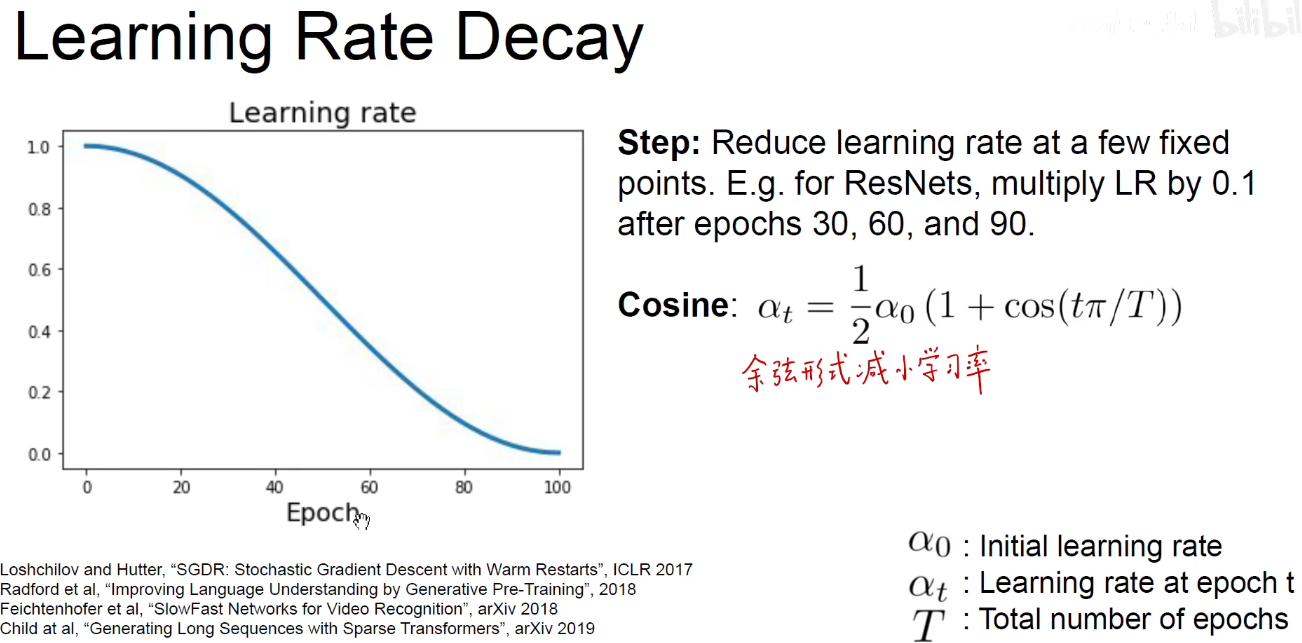
线性形式降低学习率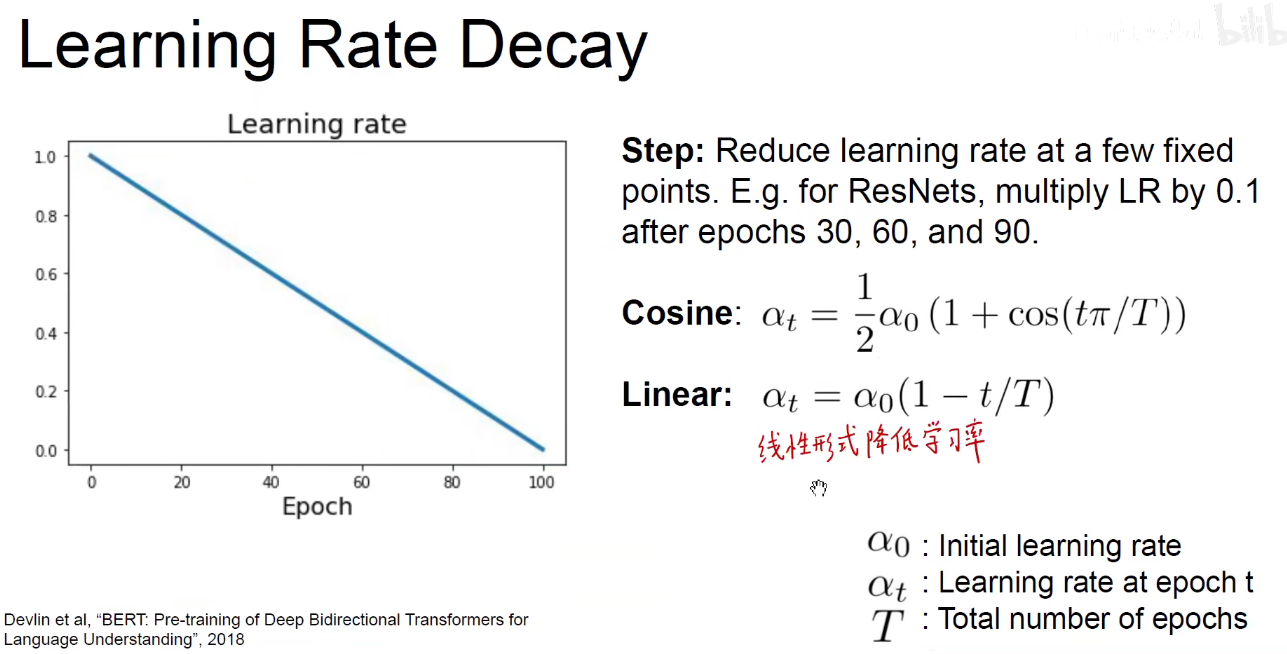
幂函数形式降低学习率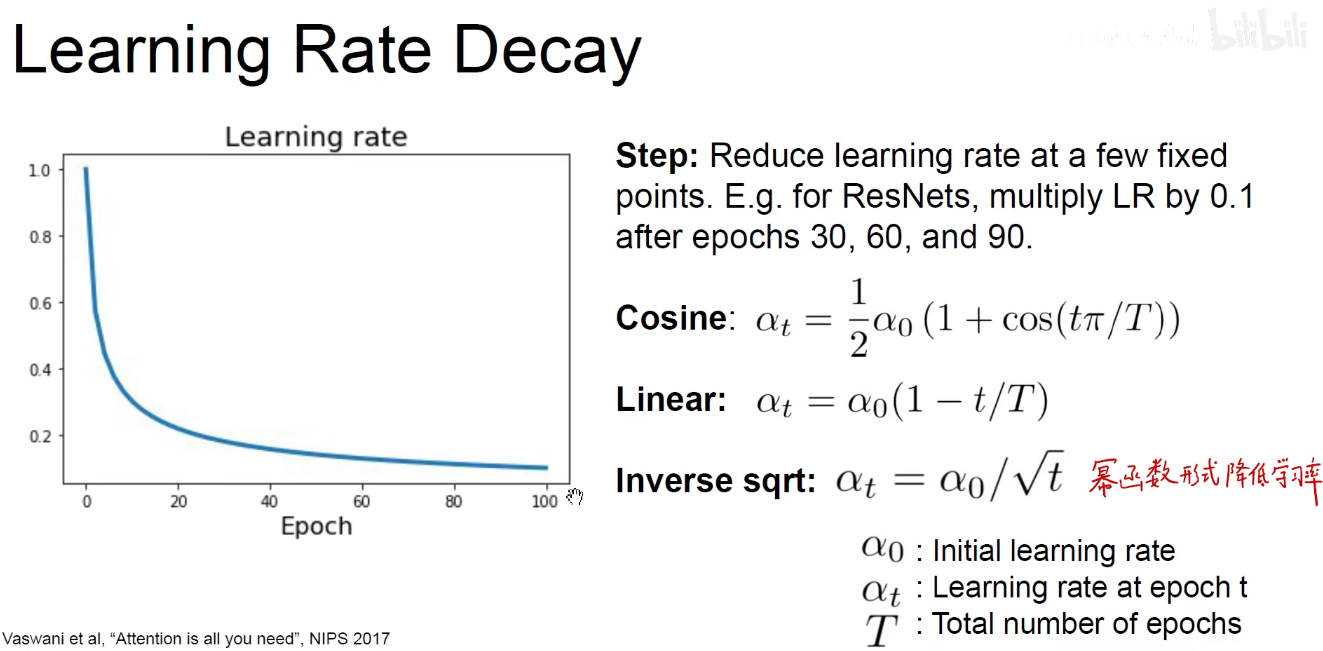
到目前讲到的都是一阶优化算法
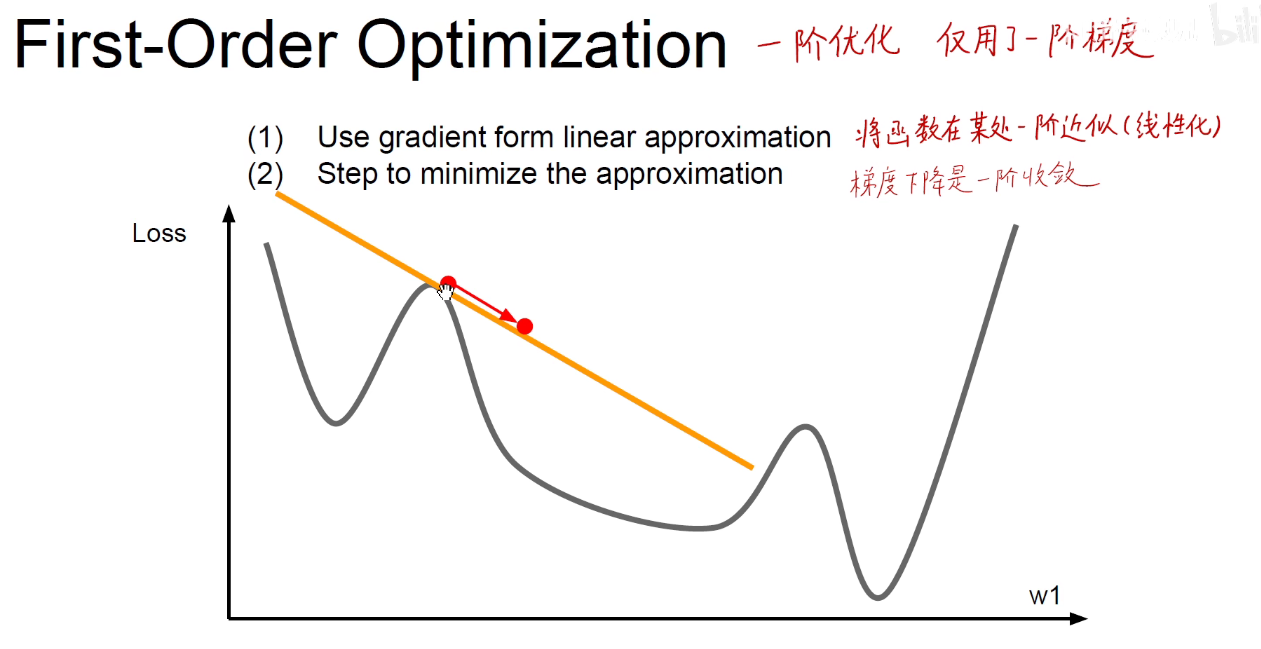
二阶优化
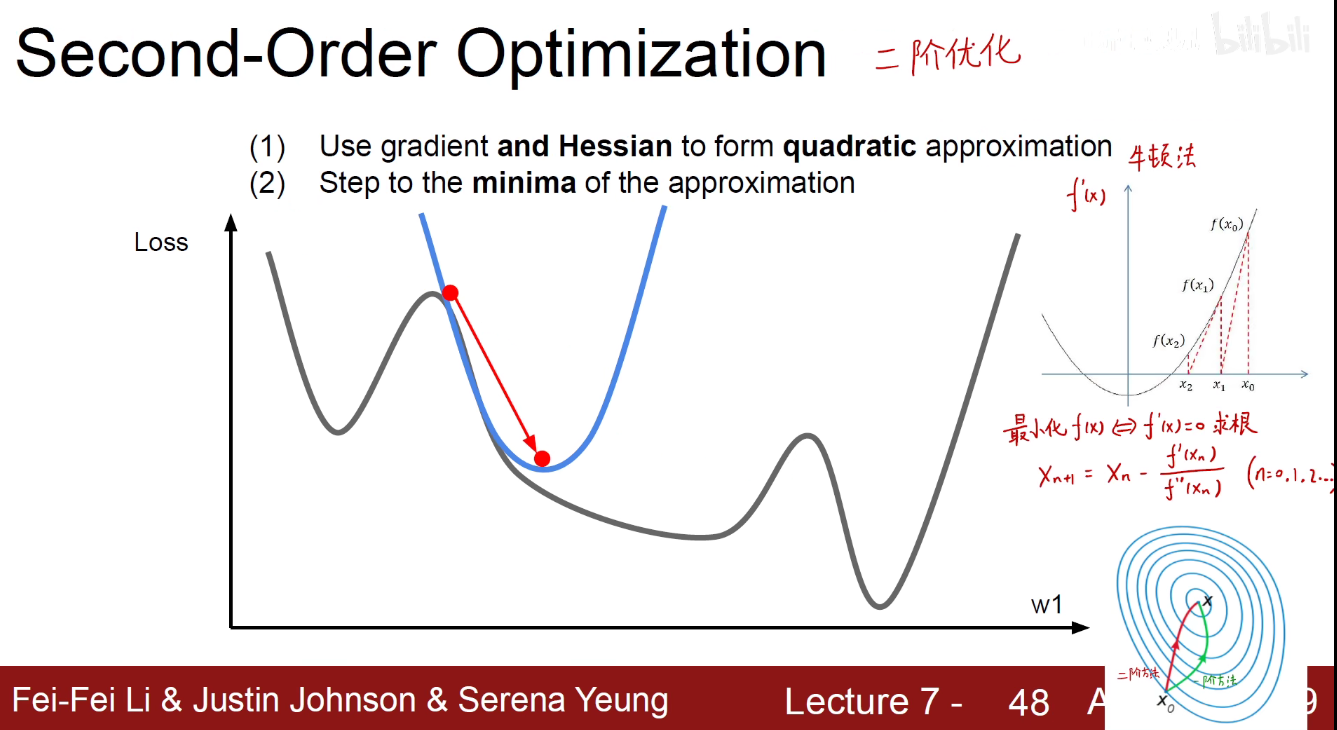
位移的一阶导数是速度,速度的一阶导数是加速度,所以位移的二阶导数是加速度。
考虑函数面的曲率,就能更快的收敛。
如图所示的牛顿法就是一个方法。纵轴是 f‘(x)

因为海森矩阵的逆矩阵难求,当参数过多,海森矩阵就会变得特别的庞大。一般不会用。

为了解决海森矩阵的问题,人们提出 BGFS方法



以上就是优化器的内容,优化器本质上就是让我们的损失函数尽快的下山,下山可以采取各种各样的策略,可以让一个胖子滚着下山,走一步看一步的下山,对梯度方向产生惩罚这样的下山,还可以综合考虑两种动量的下山,以及考虑二阶梯度的下山,但是二阶梯度要求海森矩阵的逆矩阵,这在深度学习这种参数量爆炸的情形下,计算量是跟不上的。所以我们用一阶优梯度化的方法,能够收敛到工程要求的精度既可以。
4 训练过程中的其他细节
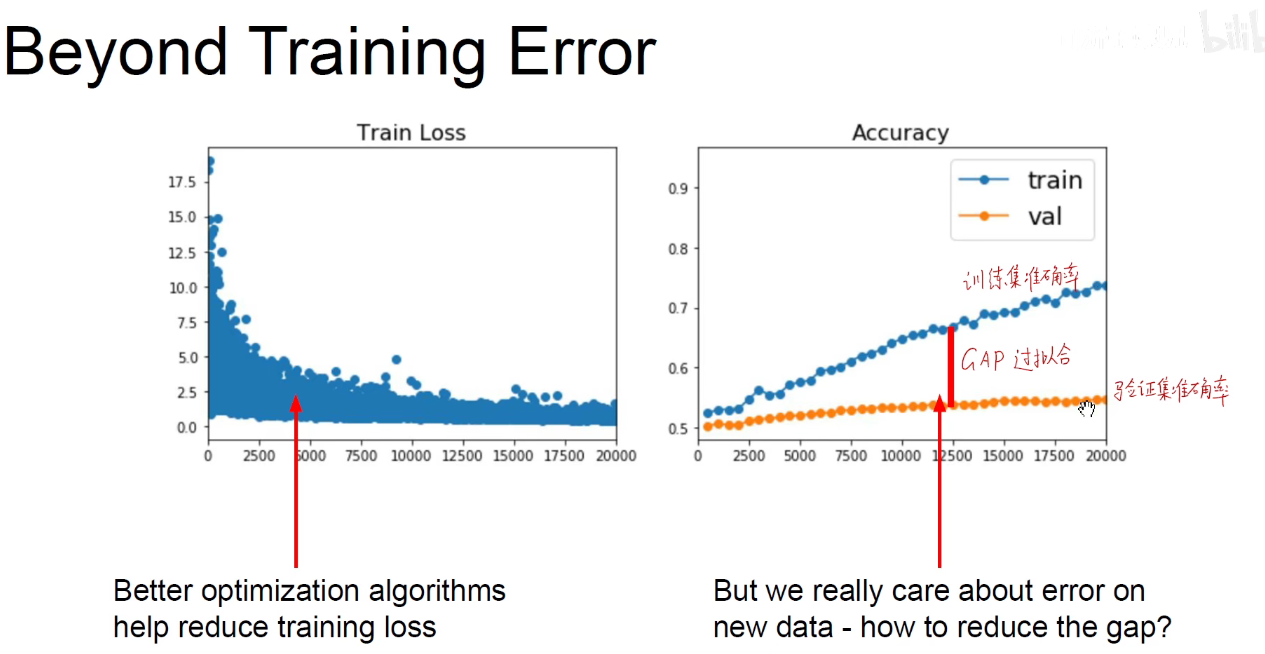
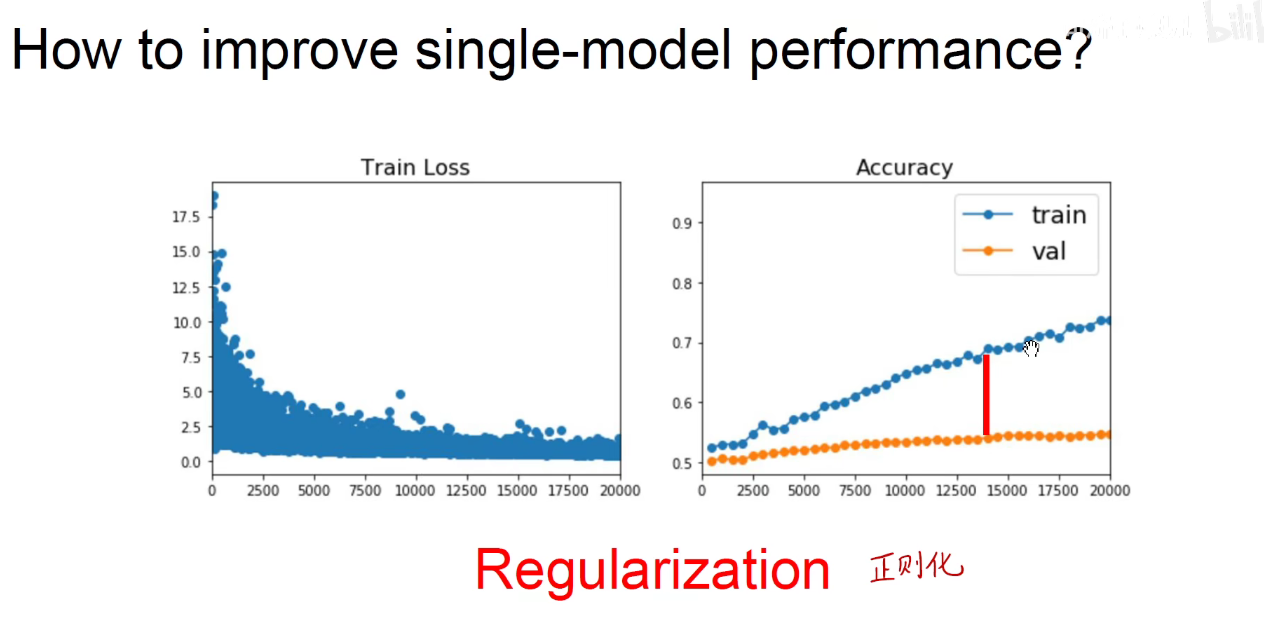
上图表示产生了过拟合。
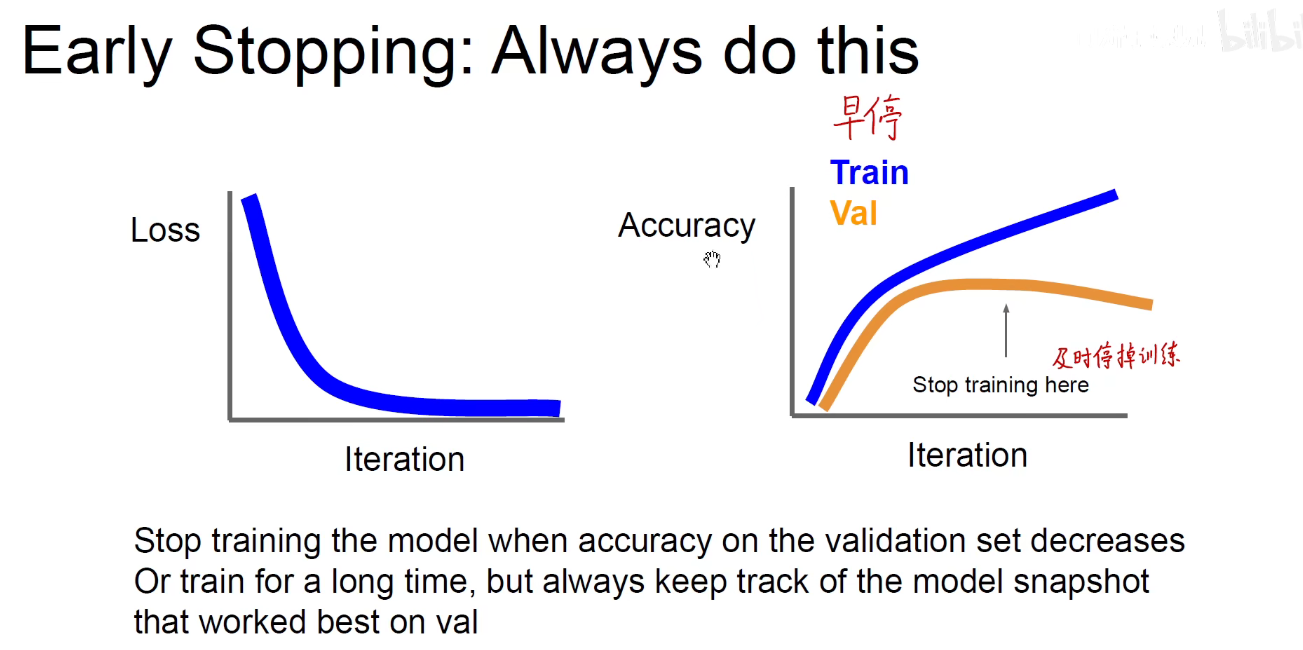
Early-Stopping: 早停
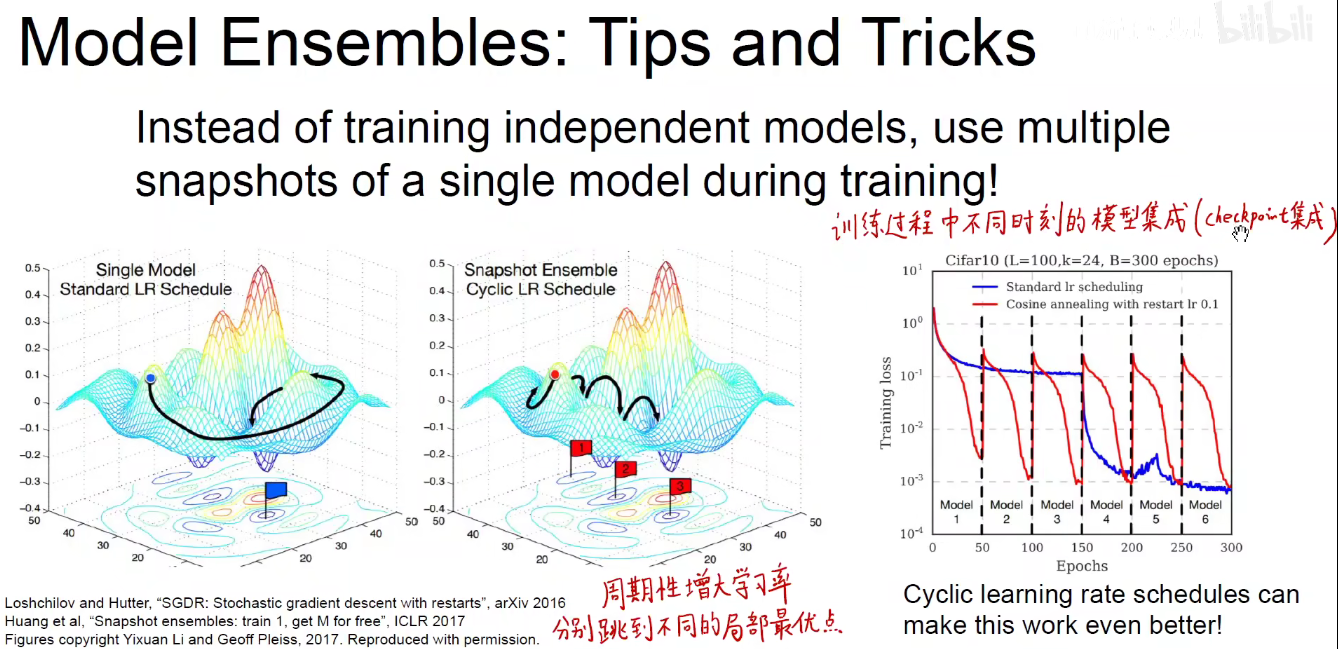
Model-Ensembles: 模型集成

5 Regularization
如何改善单个模型的性能?正则化
之前的正则化方法:L1 L2 和 二者结合的 弹性网正则化。

5.1 Dropout
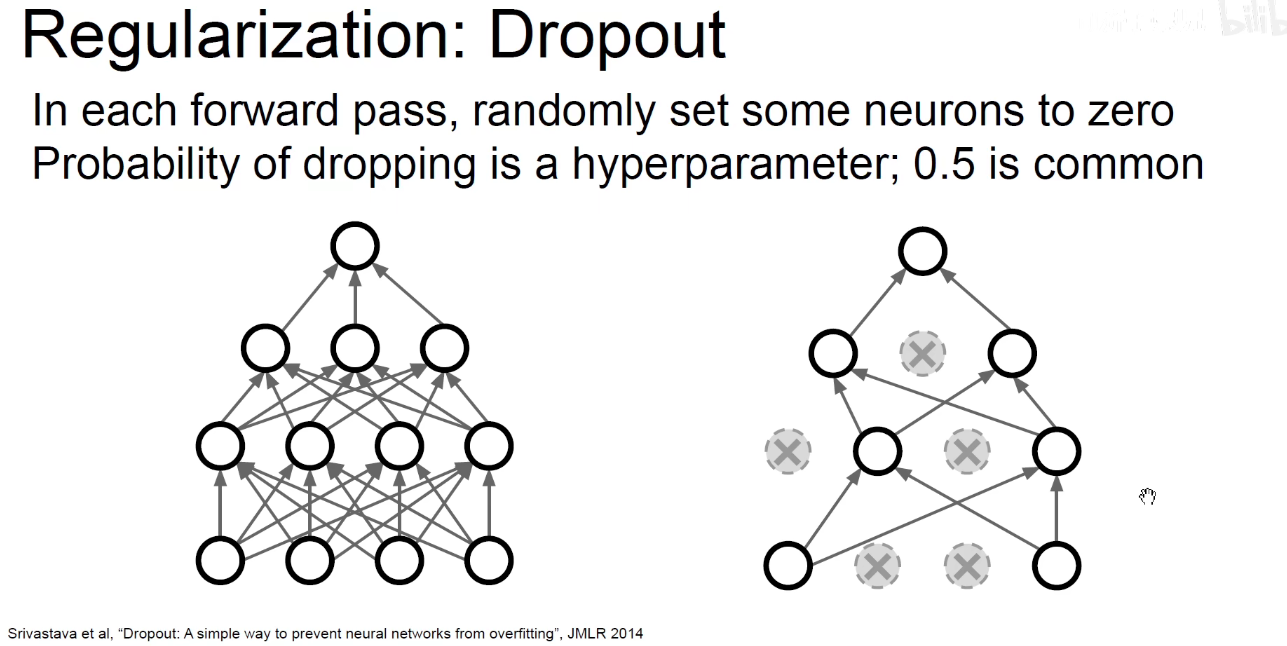
dropout-mask:像一个版,只有透着风的可以存活。

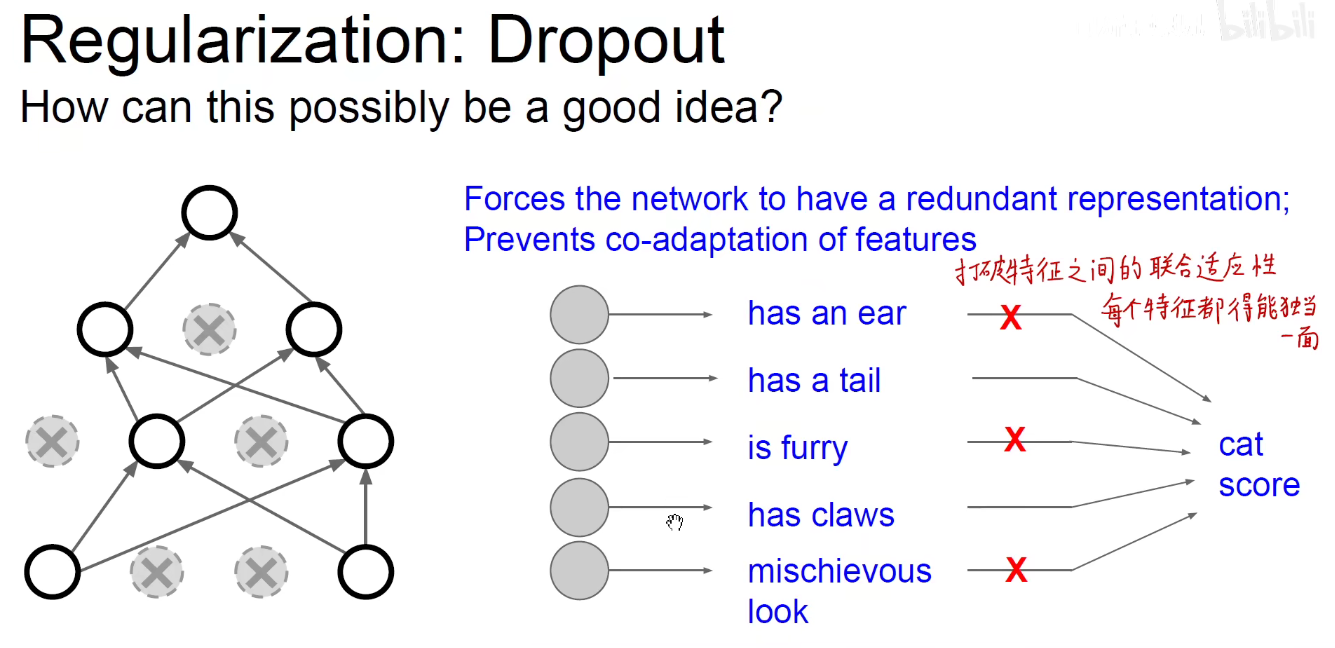
优点1如下图:打破了神经元之间的联合适应性,每个神经元都被逼着每次和不同的神经元进行协作,假设他们之前产生了依赖关系,那这个依赖关系随时都可能被抹掉,每个神经元被逼着不得不独当一面。神经元之间的依赖性消失,他们之间变得彼此独立。
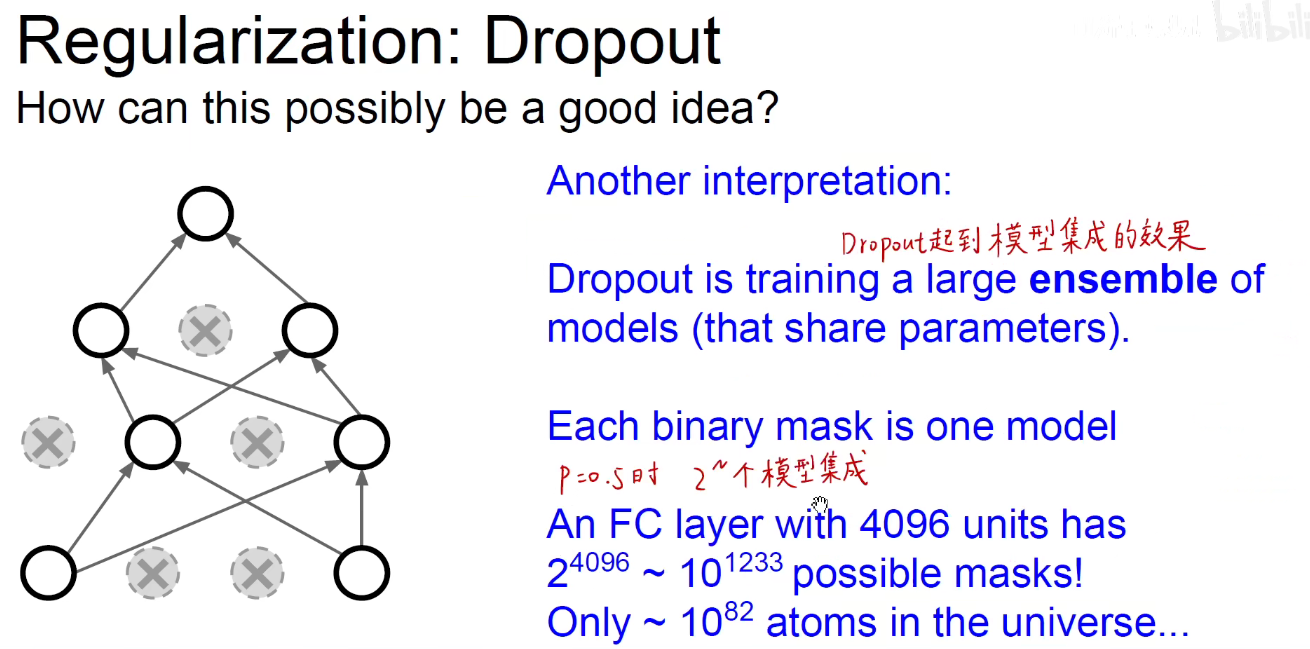
优点2如下图:起到了模型集成的效果。每一层的神经元都有0.5的概率存活。
每一步都训练模型中的子模型,而且权重和参数时共享的。
如下图:在训练阶段,对a的期望。

如下图:在测试阶段,我们不需要Dropout,需要所有逇神经元都存活,a的数学期望就是 w1x+w2y

如下图,在训练时用p的概率进行Dropout,在测试时需要将p乘上去。

Inverted Dropout:不改变测试阶段的代码,只在训练期间原地补偿校正。

Dropout为何有效?

5.2 Data Augmentation
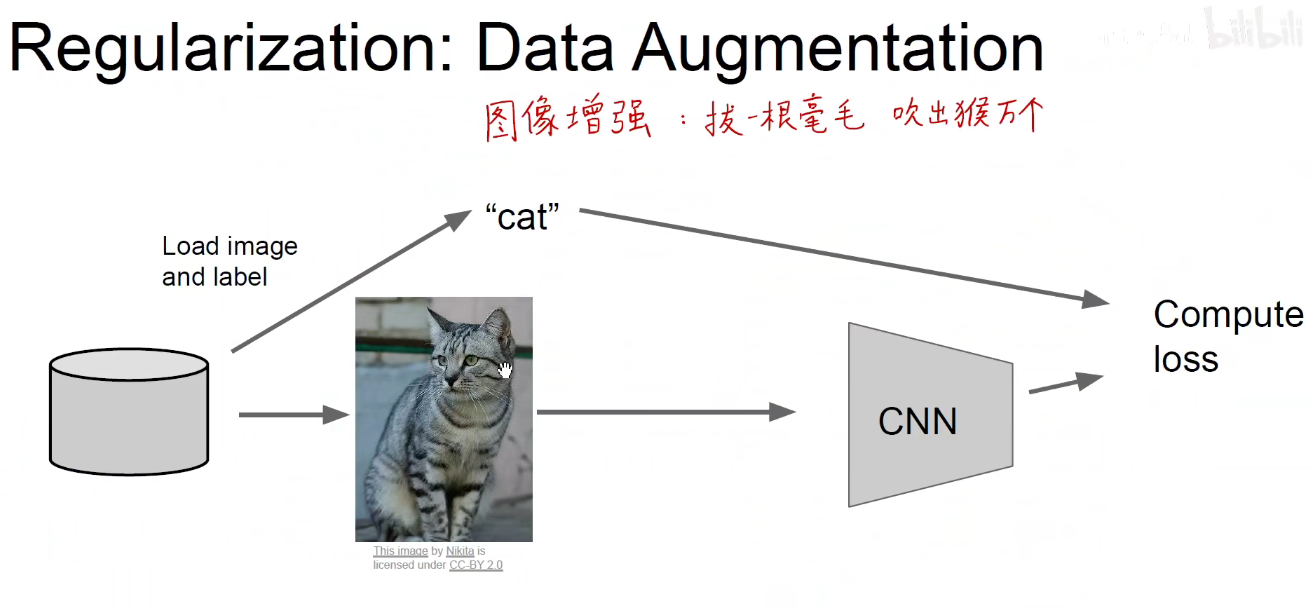
水平翻转+颜色的增强
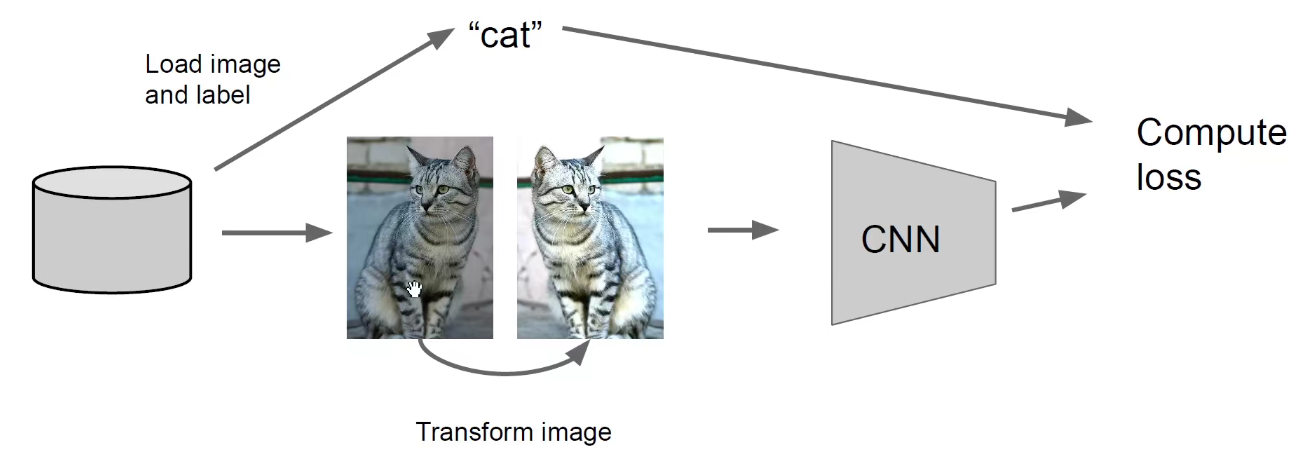
随机裁剪

像素级别的偏移

一般用到的方法

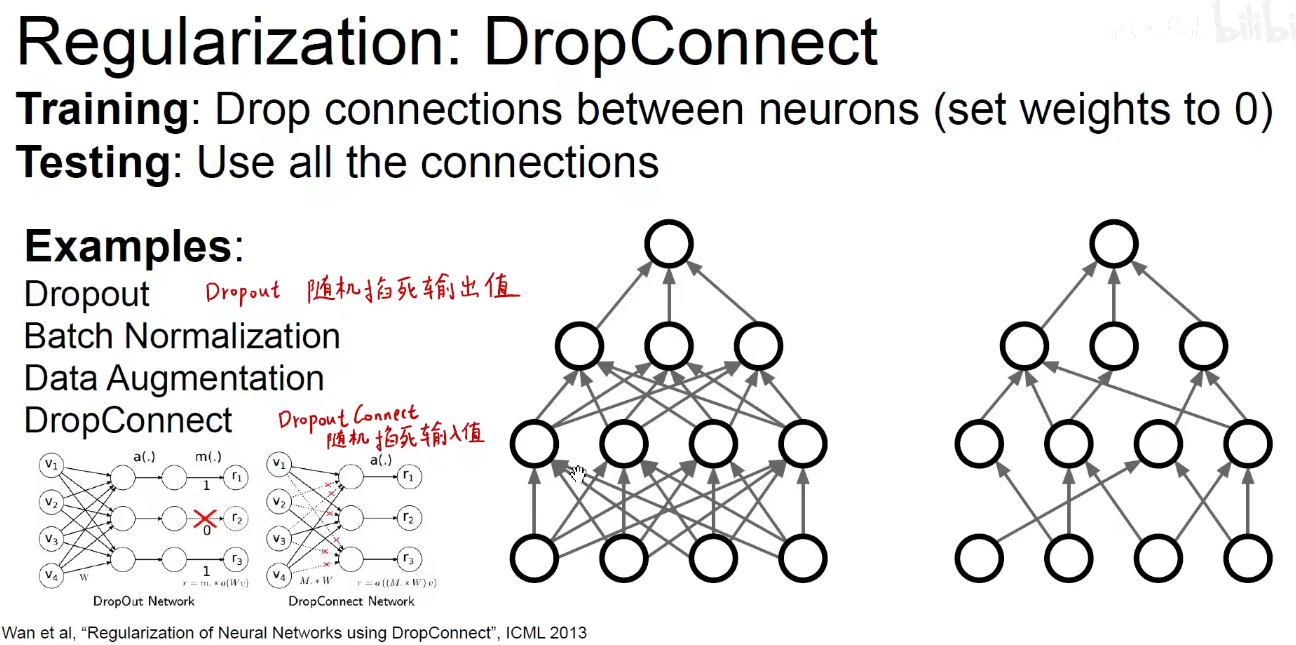
DropConnect:随机掐死输入值。Dropout:随机掐死输出值。
DropConnect: 相当于掐死了神经元的某些树突。





6 Choosing Hyperparameters-超参数选择

校验初始损失函数值,要确定损失函数在一开始时大概是什么类别的数量级,保证神经网络没有什么额外的错误。

在小参数集上尝试过拟合,一旦小参数集发生过拟合,往往意味着大参数集也是过拟合的,可以进行很好的优化。
找到能使损失函数快速下降的学习率,一般采用0.1,0.01,0.001,0.0001来进行学习率的尝试。

权重衰减尝试使用 1e-4, 1e-5

一开始使用粗糙的学习率,到后面微调学习率,看看损失函数的图像曲线有没有什么变化,需不需要进行早停,有没有发生过拟合。

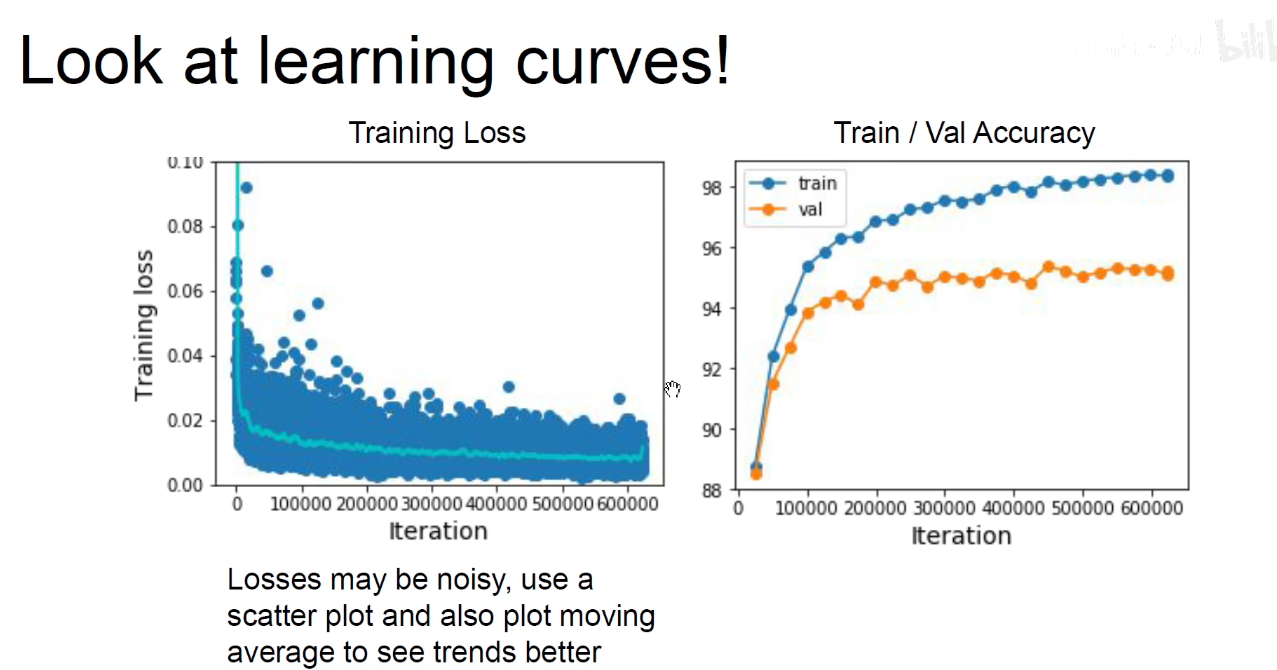
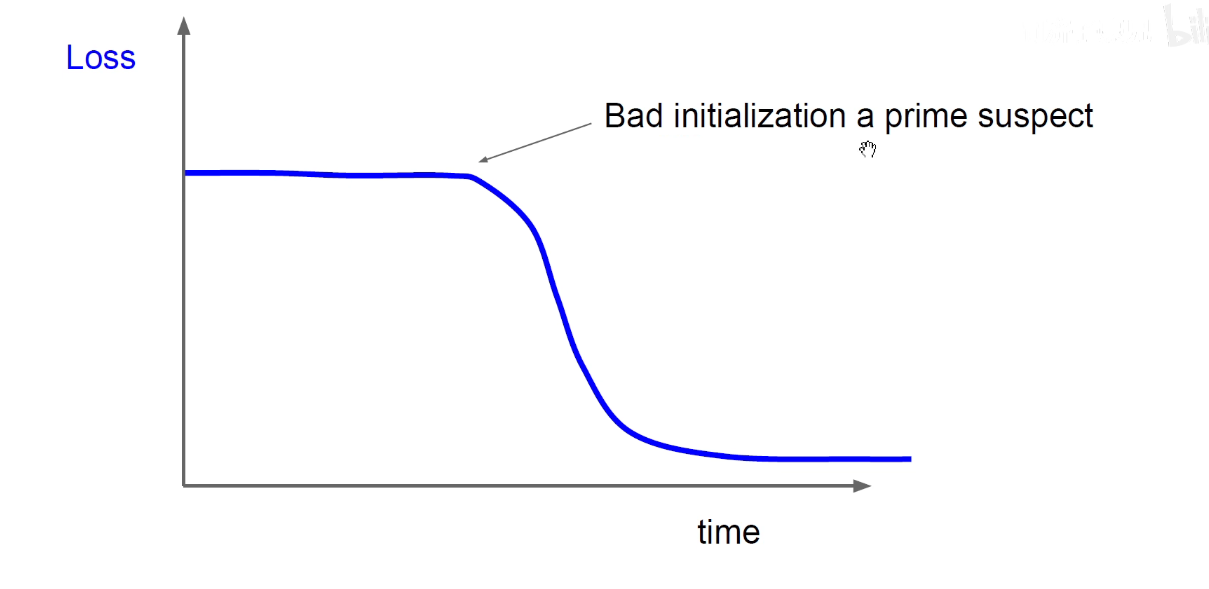
像上图,一开始的时候损失函数不怎么变化,随着时间突然降低,说明初始化不好,很可能困在了鞍点或者局部最优点。
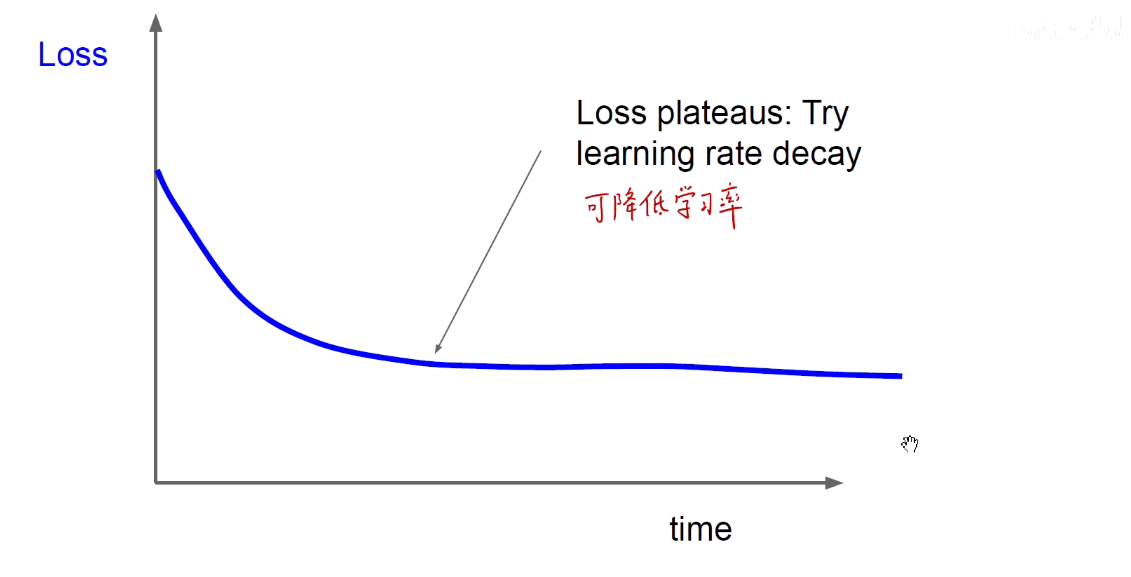
上图可降低学习率,让他沉下心来精耕细作。
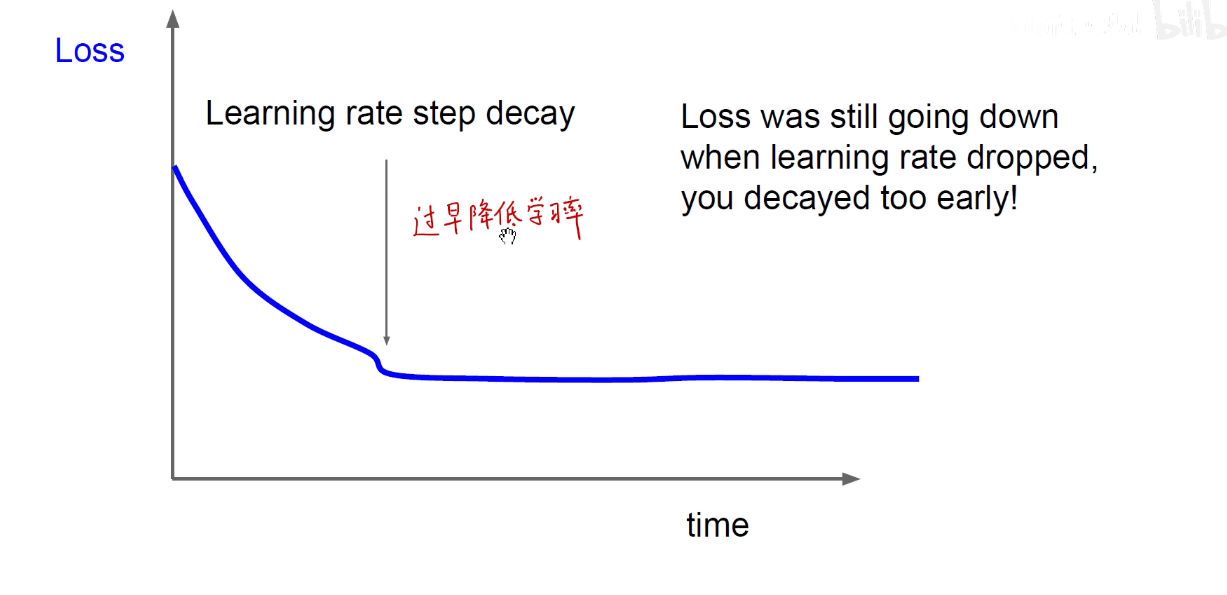
上图过早的降低学习率是不对的,应该到达瓶颈再降低。
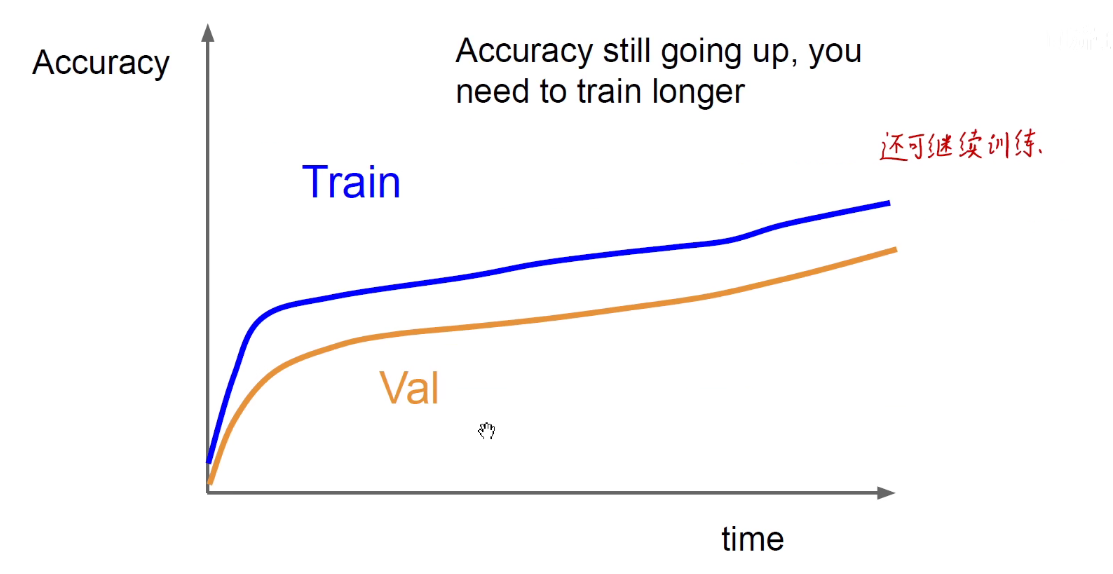
上图还可继续训练。
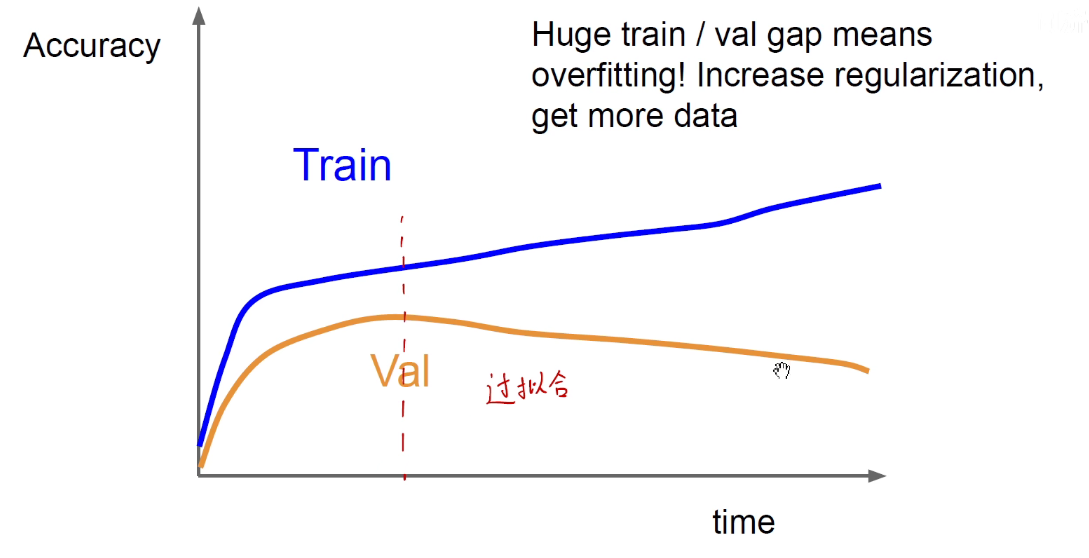
过拟合,验证集降低,可以通过正则化,获取更多的数据。
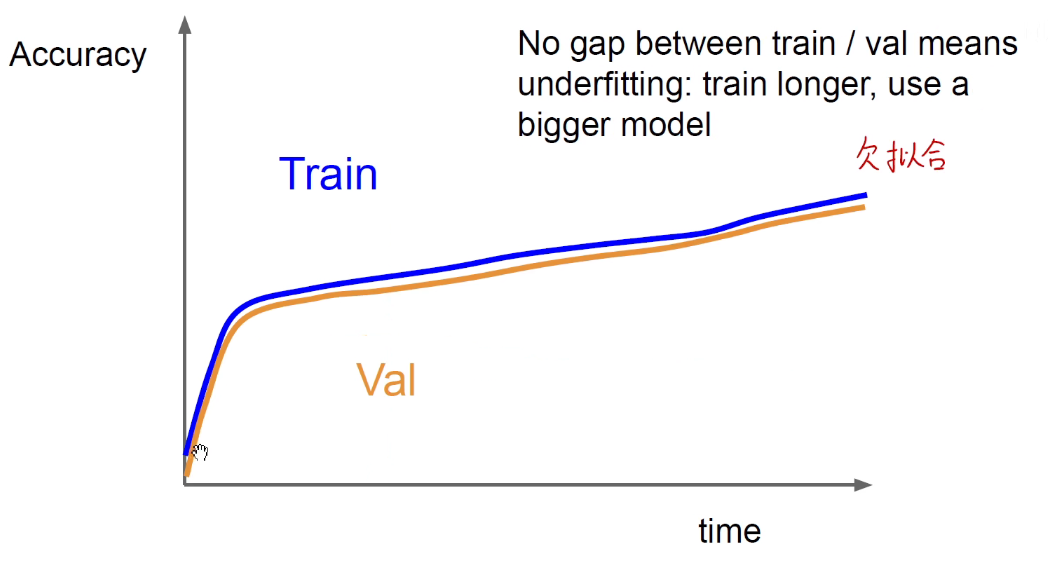
欠拟合,用更深更大的模型训练。


目前一个热门的领域是Auto ML,自动机器学习,即用机器学习的方法进行机器学习。

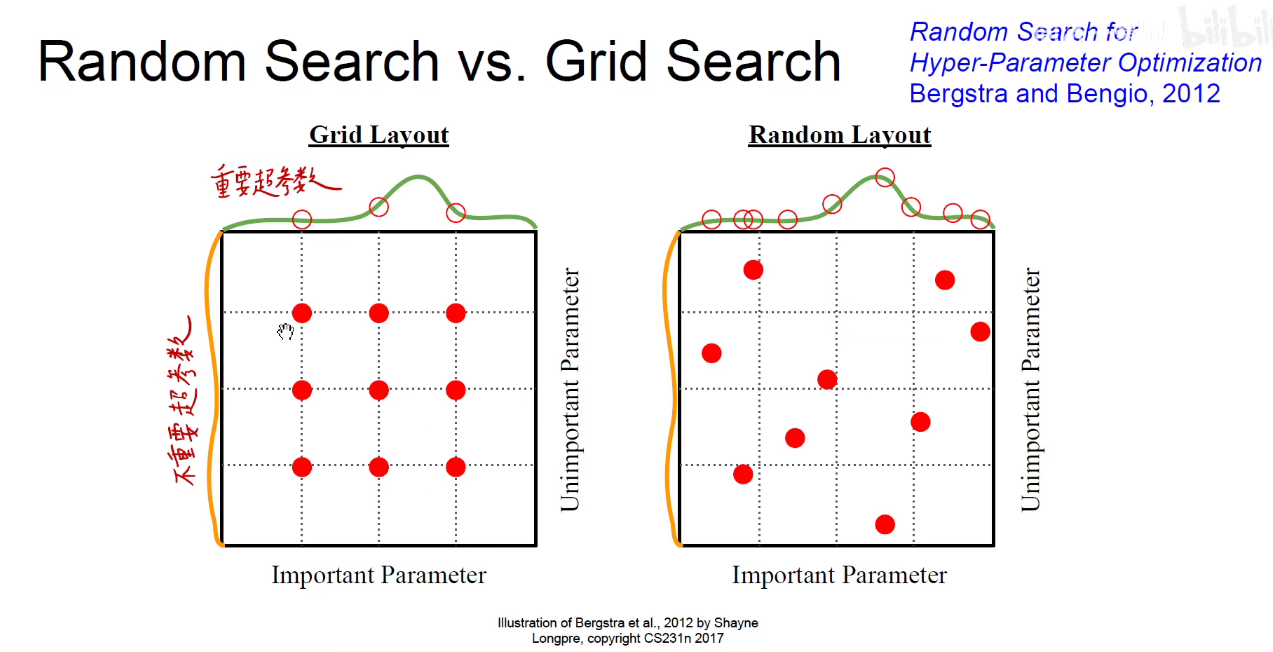
对超参数进行网格搜索或随机采样。
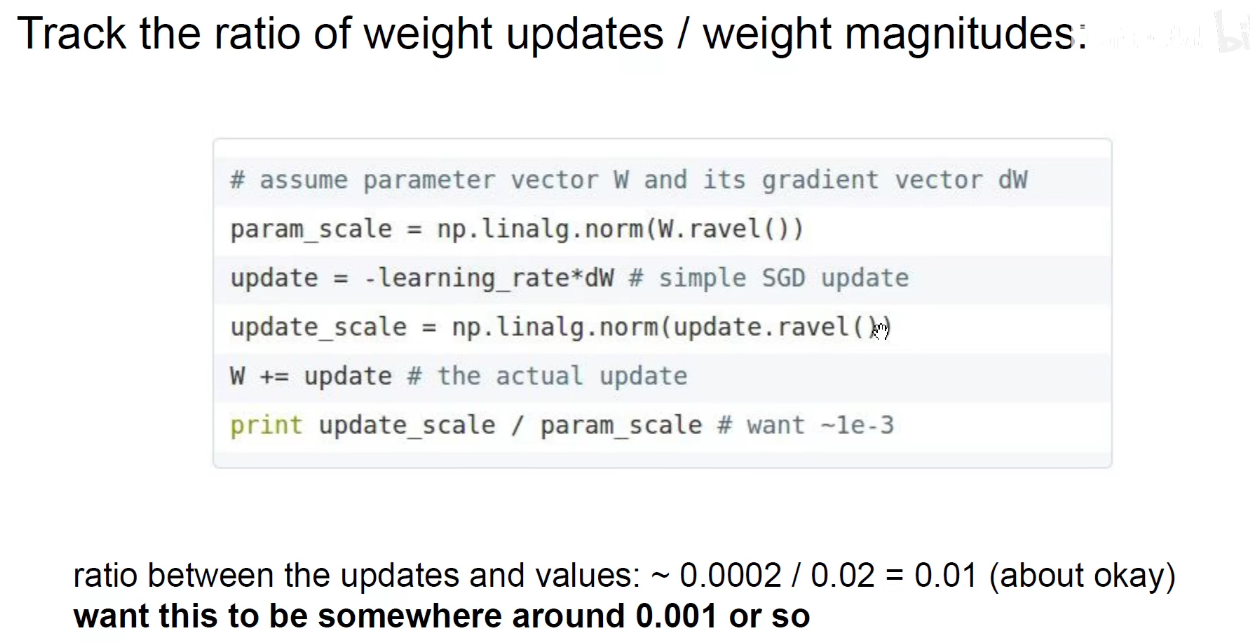
密切关注权重的更新量。
7 总结

优化算法:如何下山更快。
学习率调整:开始迈大步,后面迈小碎步。
正则化:防止过拟合,让模块可独立工作,打破他们之间的相互依赖。
超参数选择