Author: haoransun
WeChat: SHR—97
图片&知识点来源:CS231N
1 前言
聚焦一个问题,如何加速深度学习,特别是卷积神经网络的运算。即卷积神经网络的工程实践中是如何对它加速的。会从各个切入点去分析这个问题。
构建轻量化模型
改进卷积层的结构
改进卷积算法本身,加速矩阵运算
压缩权重-压缩精度–压缩模型-对模型进行剪枝
强大算力的硬件进行并行和分布式的运算
硬件、集成电路、算法、数据结构、数学方法、信号处理、通信原理以及分布式计算和嵌入式开发,结合计算机视觉的CNN运算。

2 卷积运算-How to stack convolutions
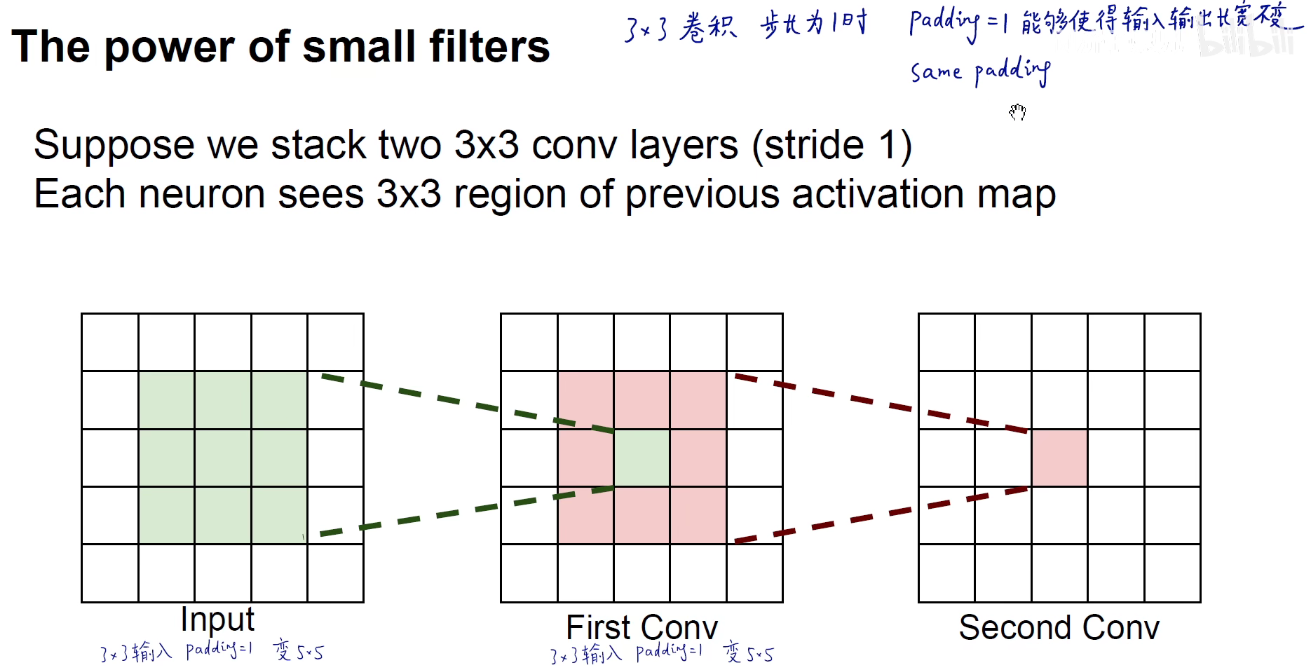
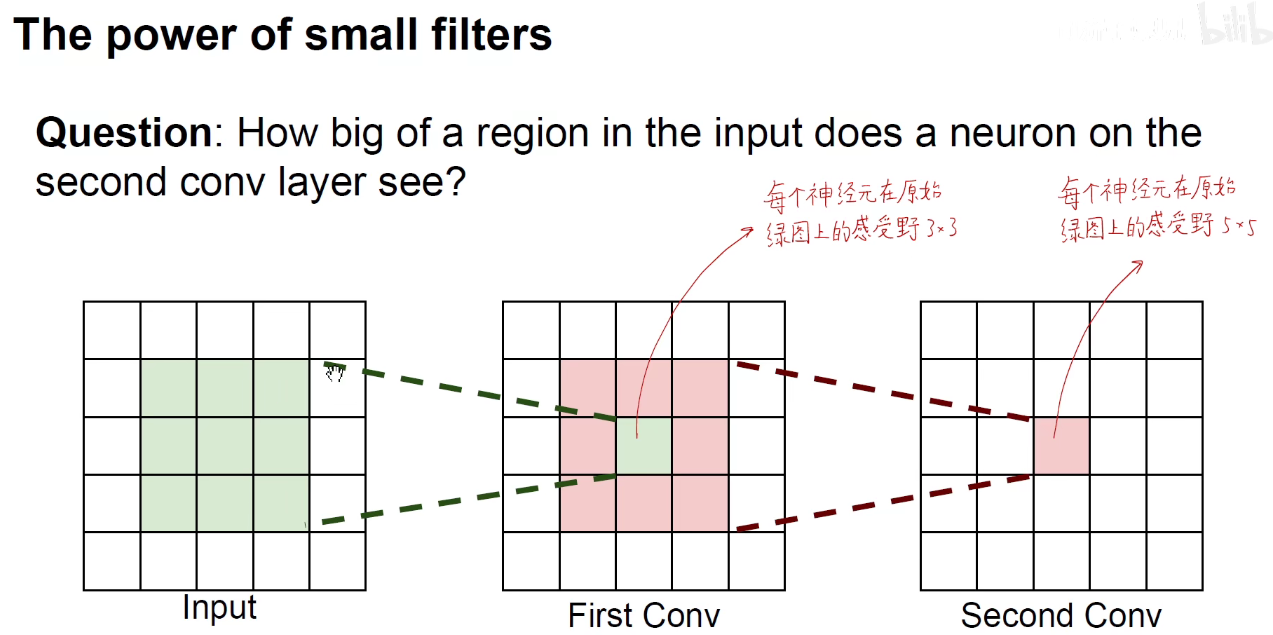
可以用两个3x3卷积来代替一个5x5卷积。
第一层卷积核感受野:3,就是卷积核本身大小
第二层卷积核感受野:3 + (3 - 1 ) = 5,即 RF2 = RF1 + (RF2 -1)
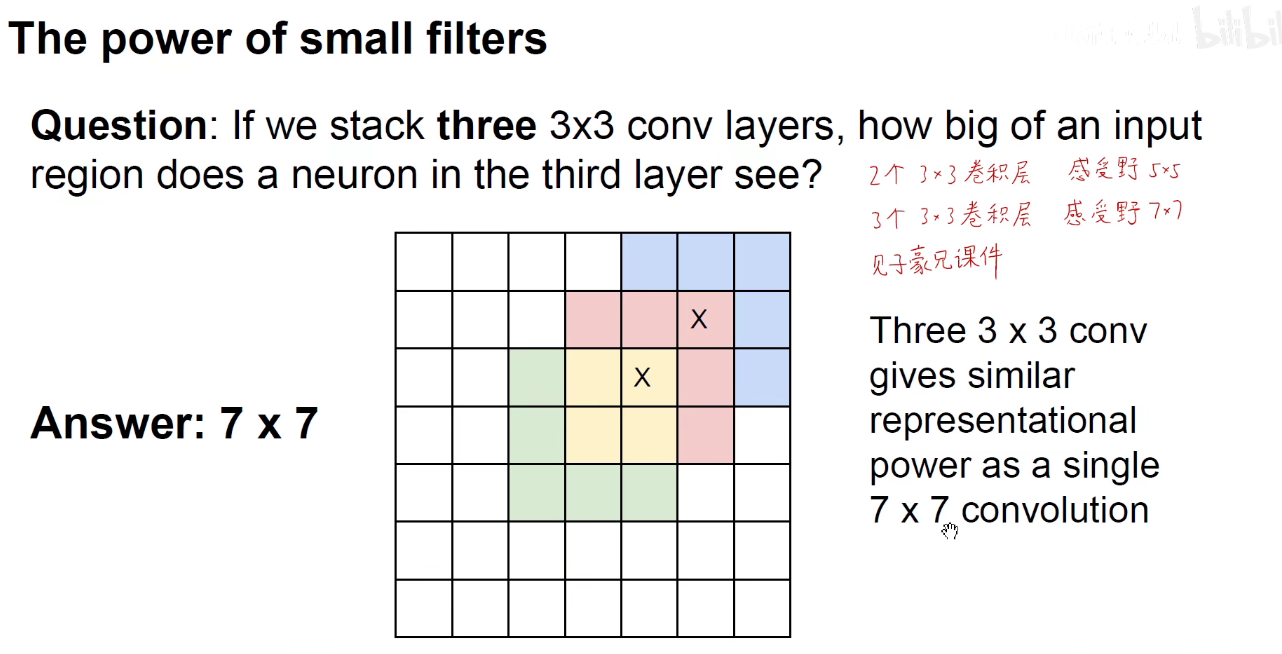
第一层卷积核感受野:3,就是卷积核本身大小
第二层卷积核感受野:3 + (3 - 1 ) = 5,即 RF2 = RF1 + (RF2 -1)
第三层卷积核感受野:5 + (3 - 1 ) = 7,即 RF3 = RF2 + (RF3 -1)
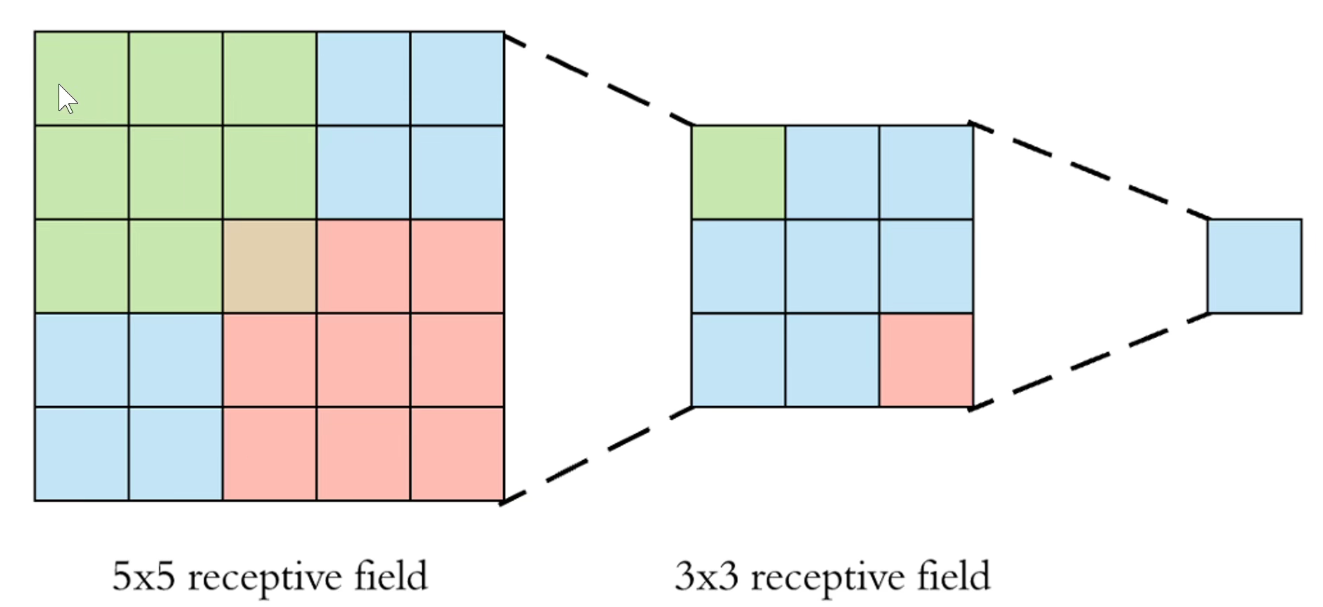
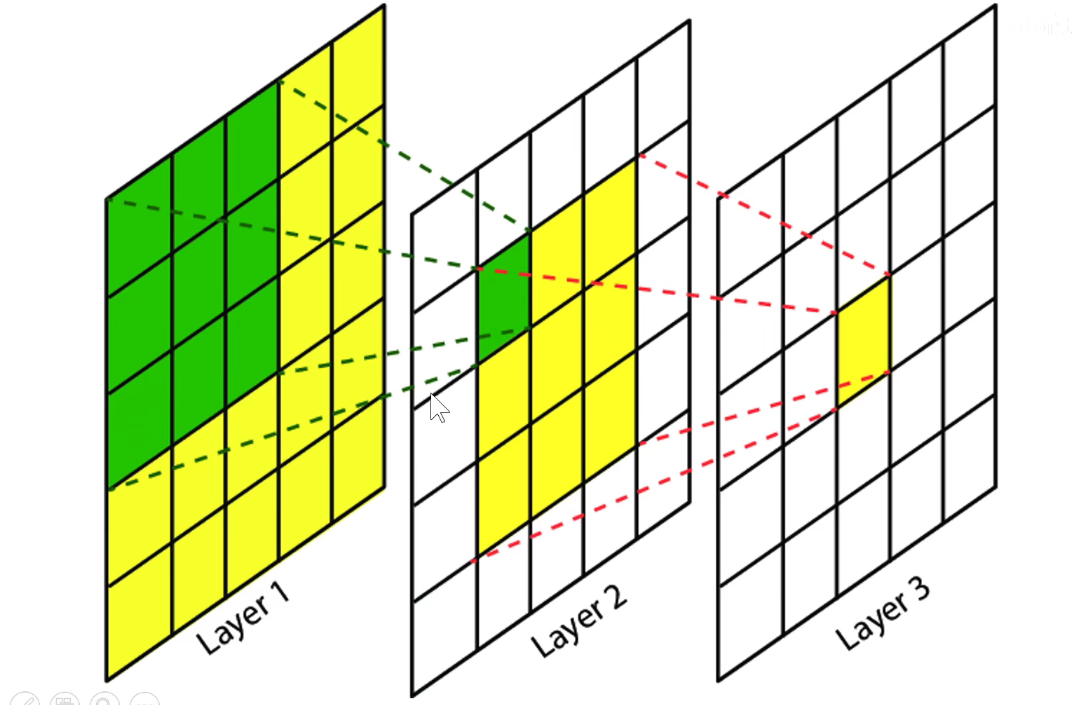
如果我们用两个3x3卷积来代替1个5x5卷积,不仅带来了参数量上的减少,更带来了非线性变换的增多。



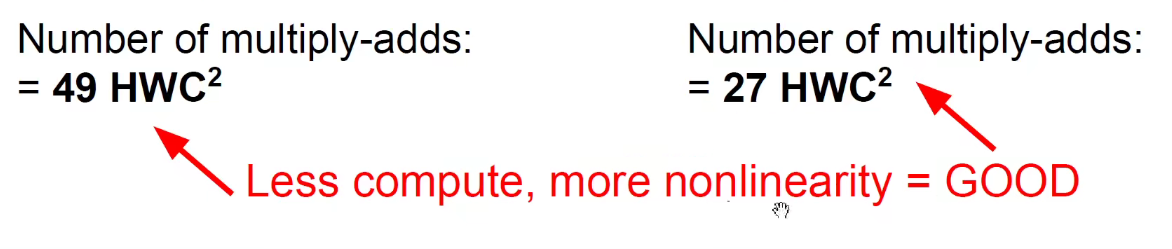

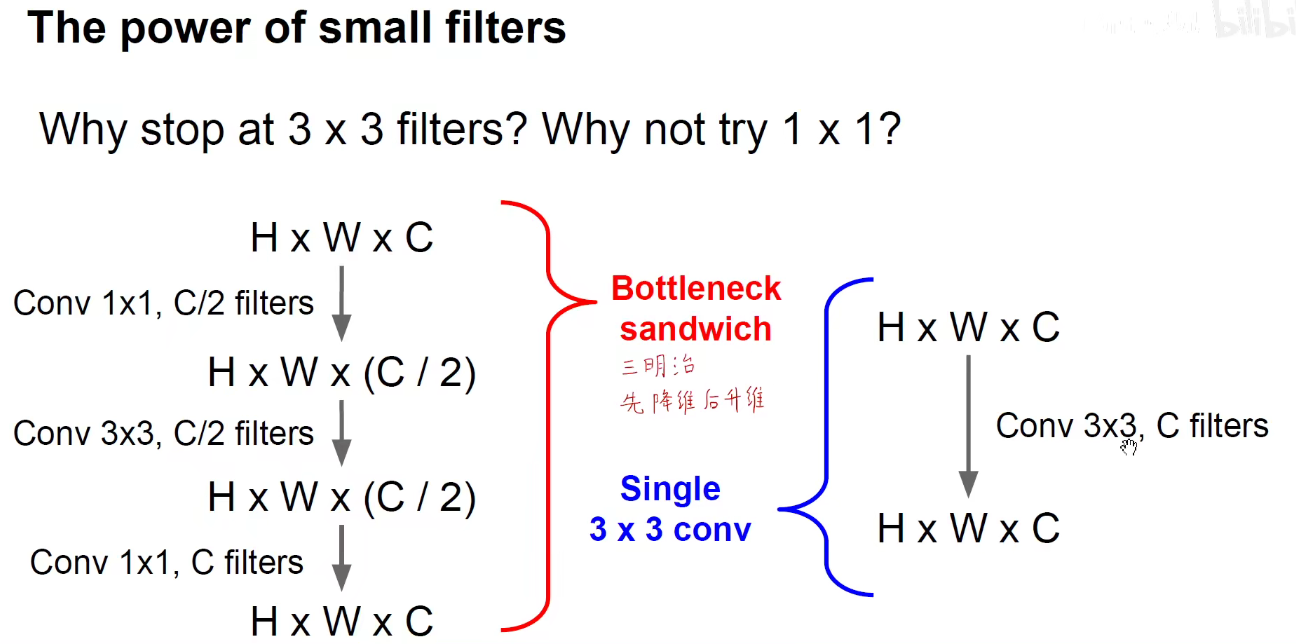

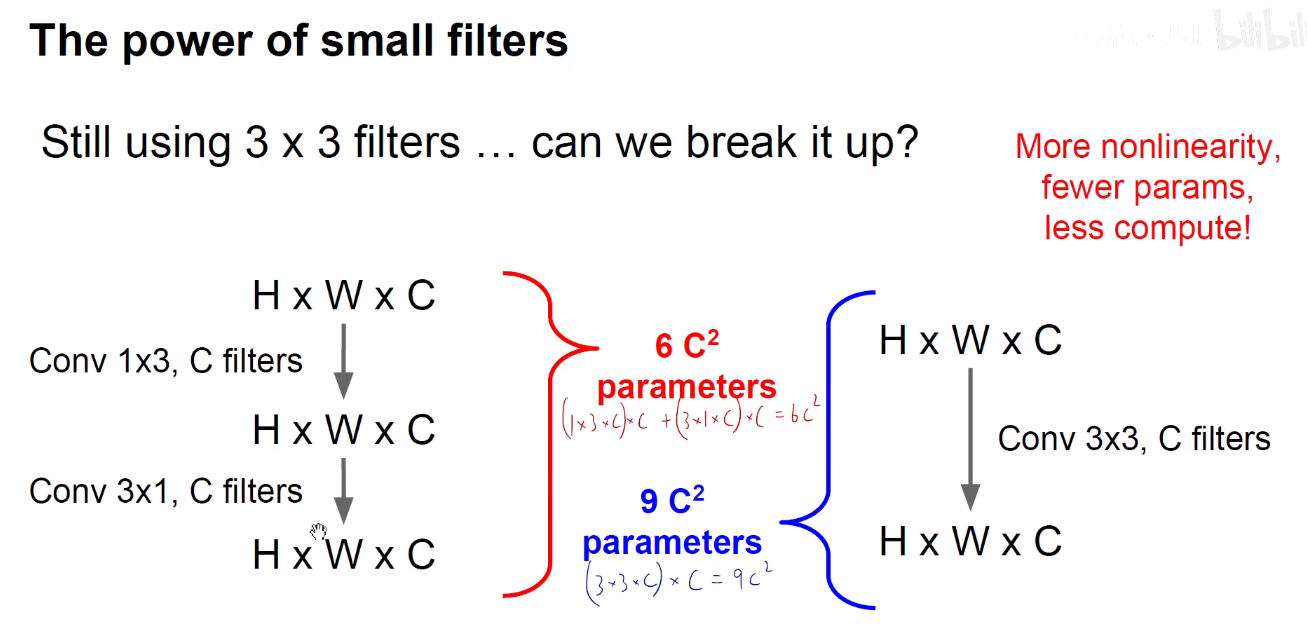
5x5卷积变成2个3x3卷积,可以分别沿宽度和深度进行拆分
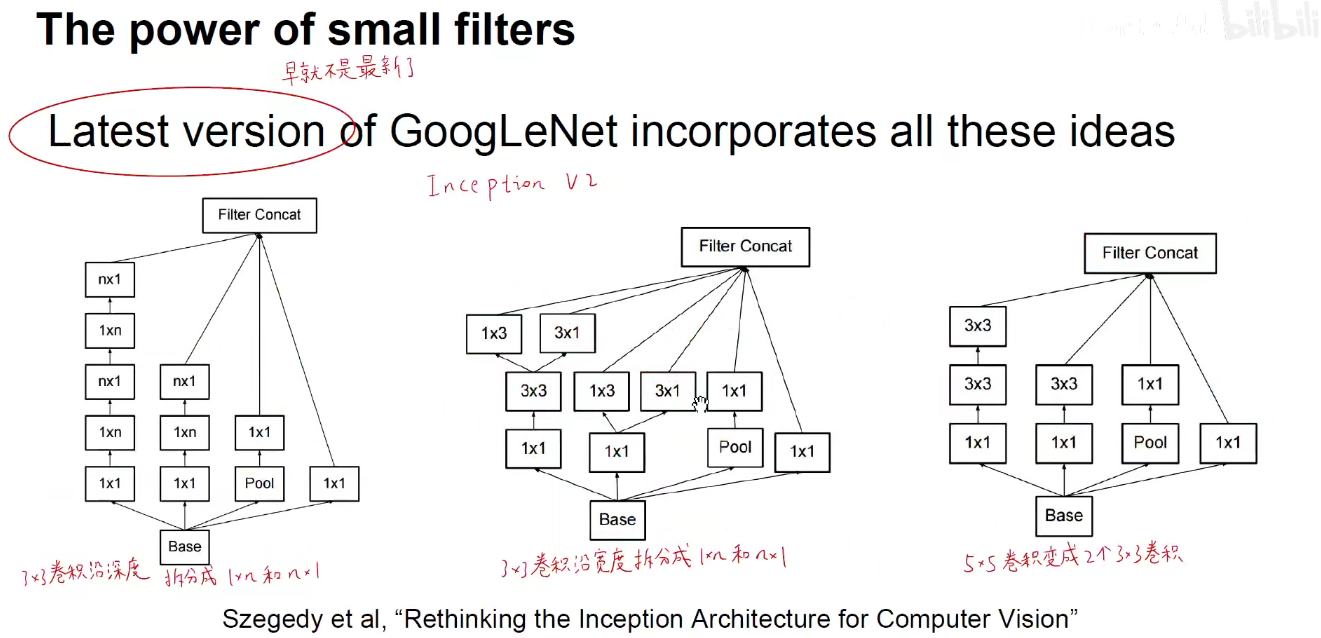

3 高效计算卷积-How to compute ConvNets-卷积加速

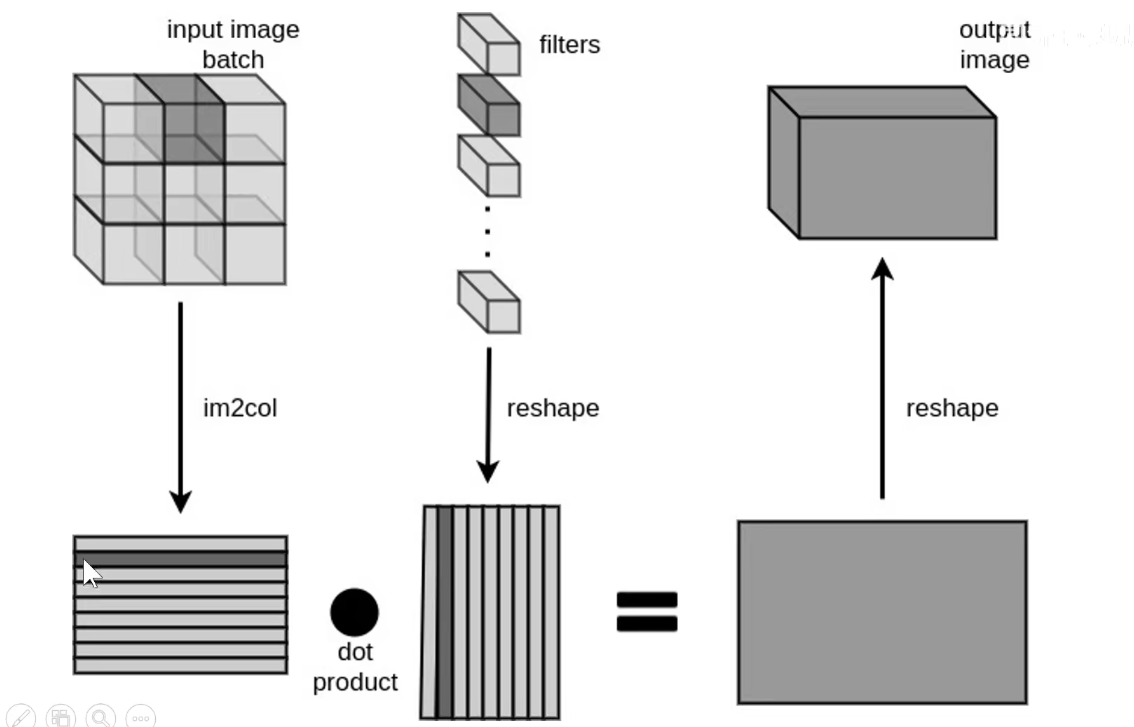
3.1 im2col
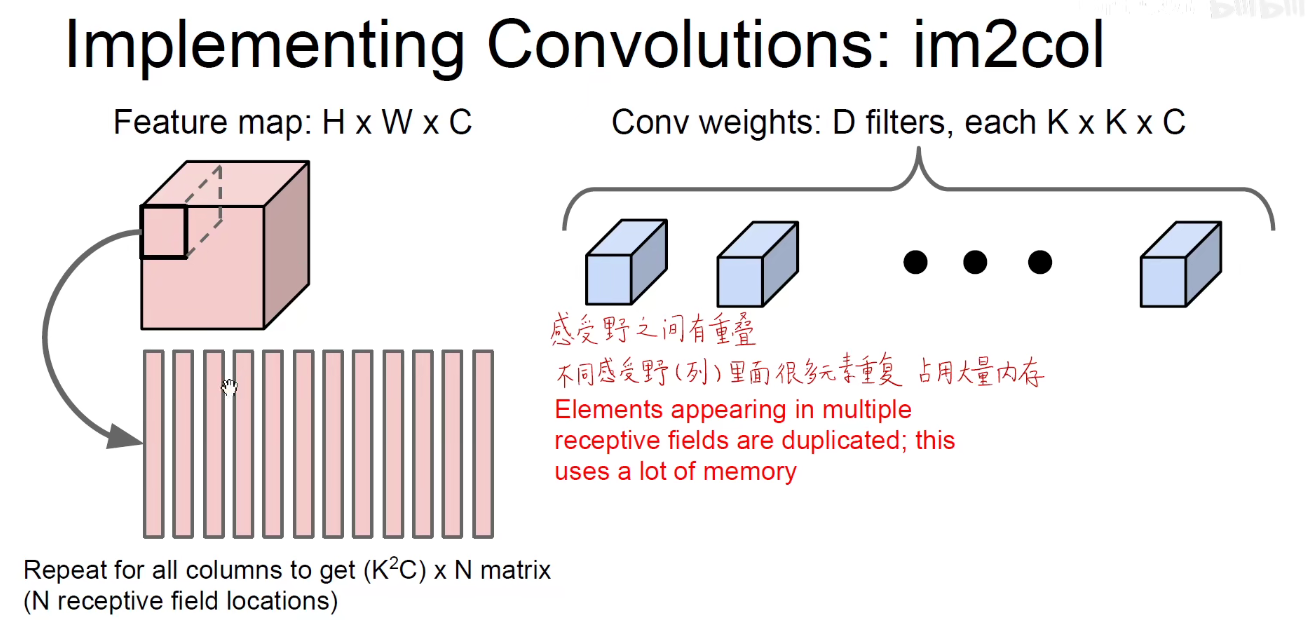
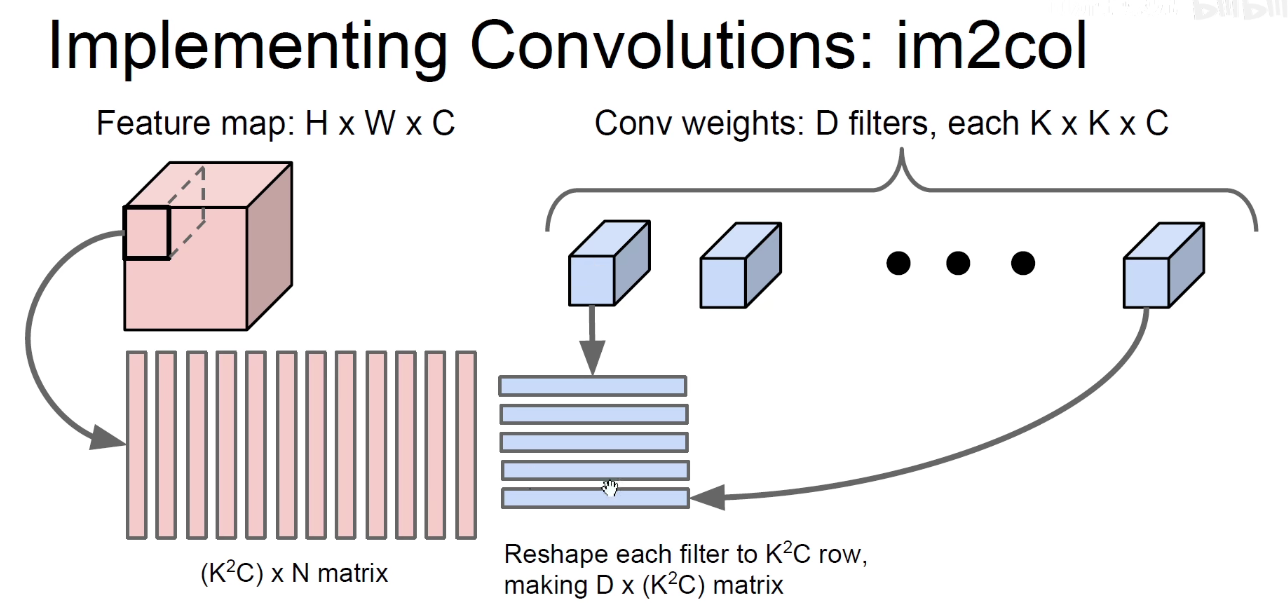
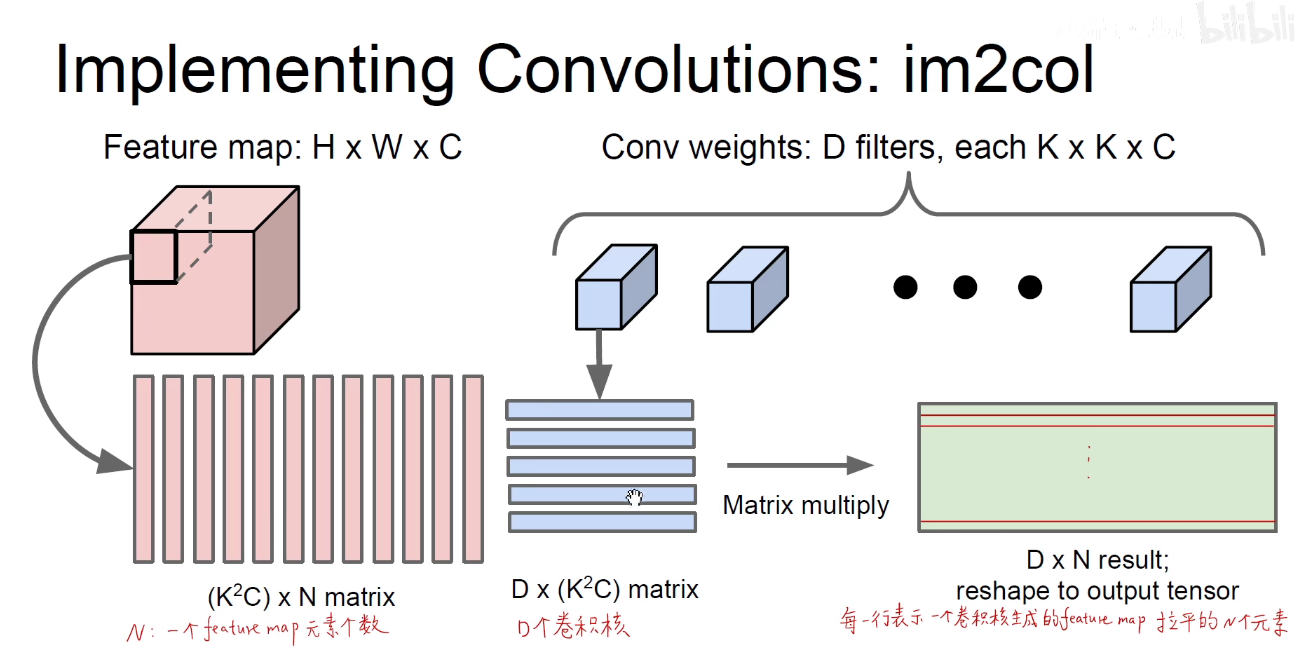
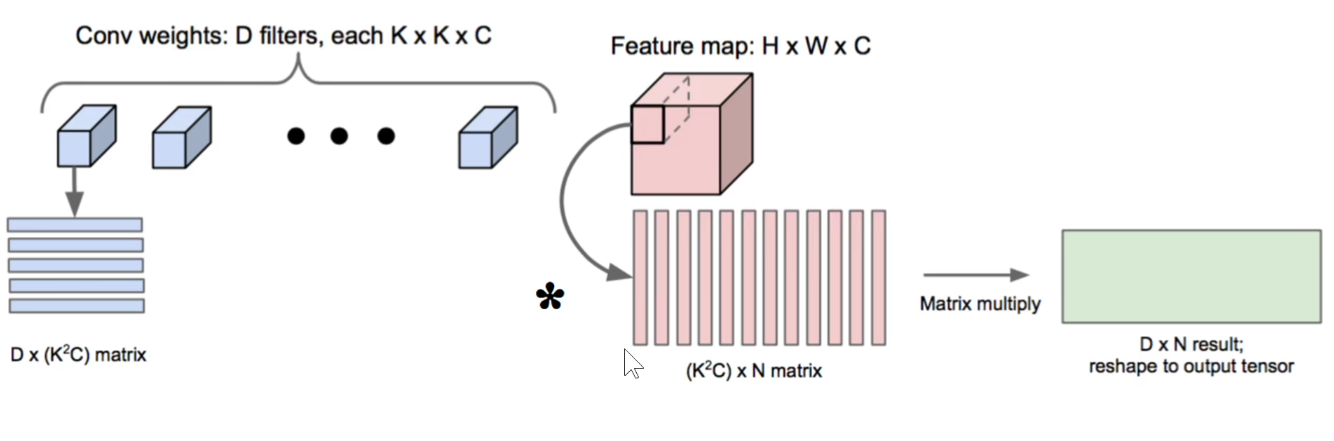
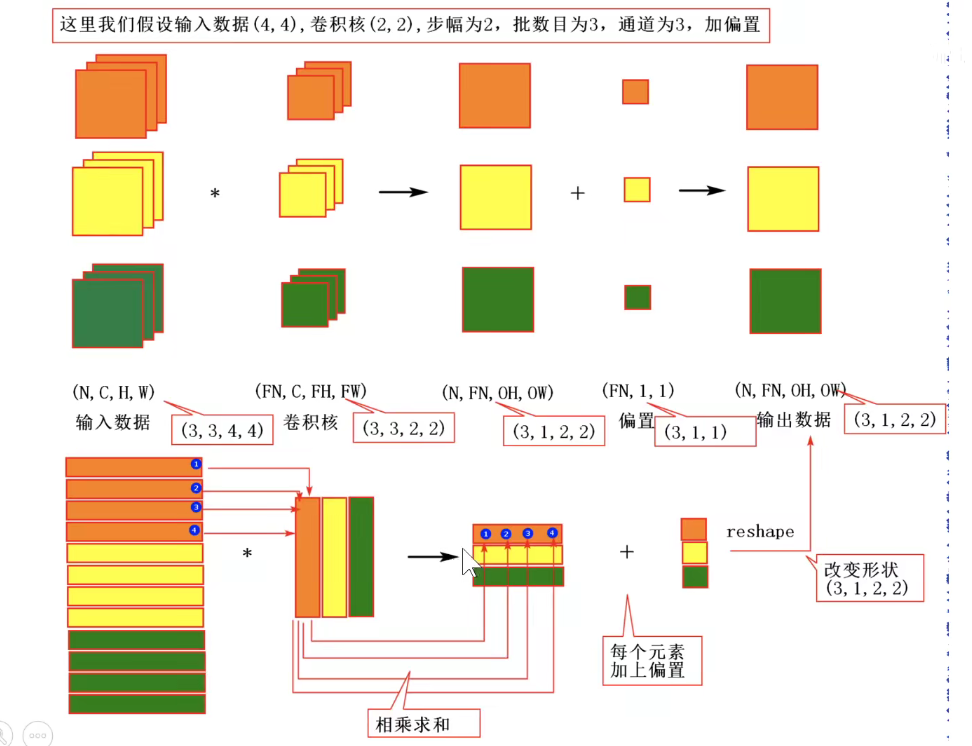
上图其实有点问题,下图才是正确的:每一行表示一个卷积核,即卷积核被拉成一行一行的,感受野拉成一列一列的。矩阵乘法:蓝色矩阵x红色矩阵得到 D x N results。
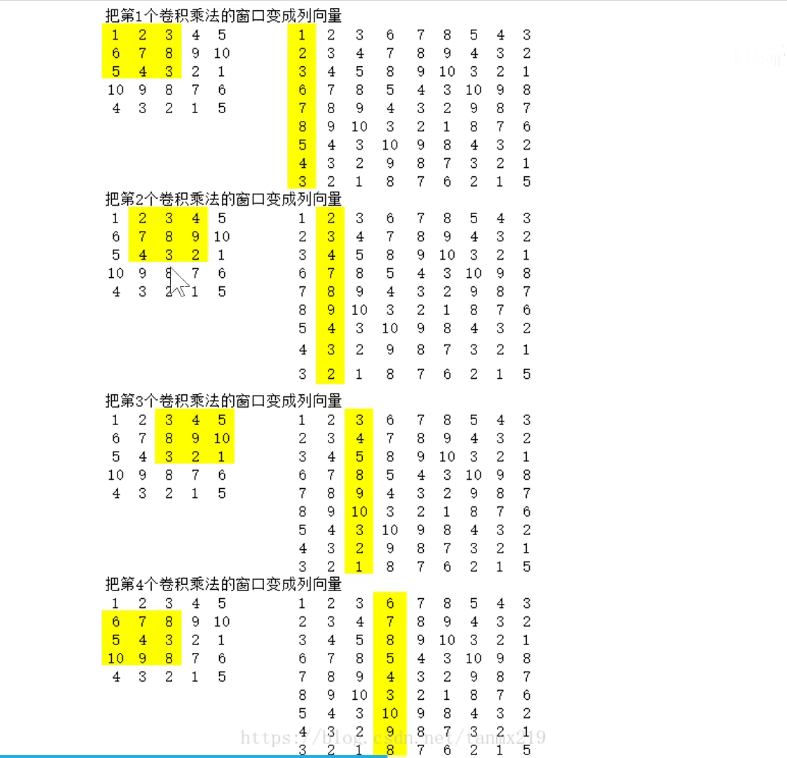
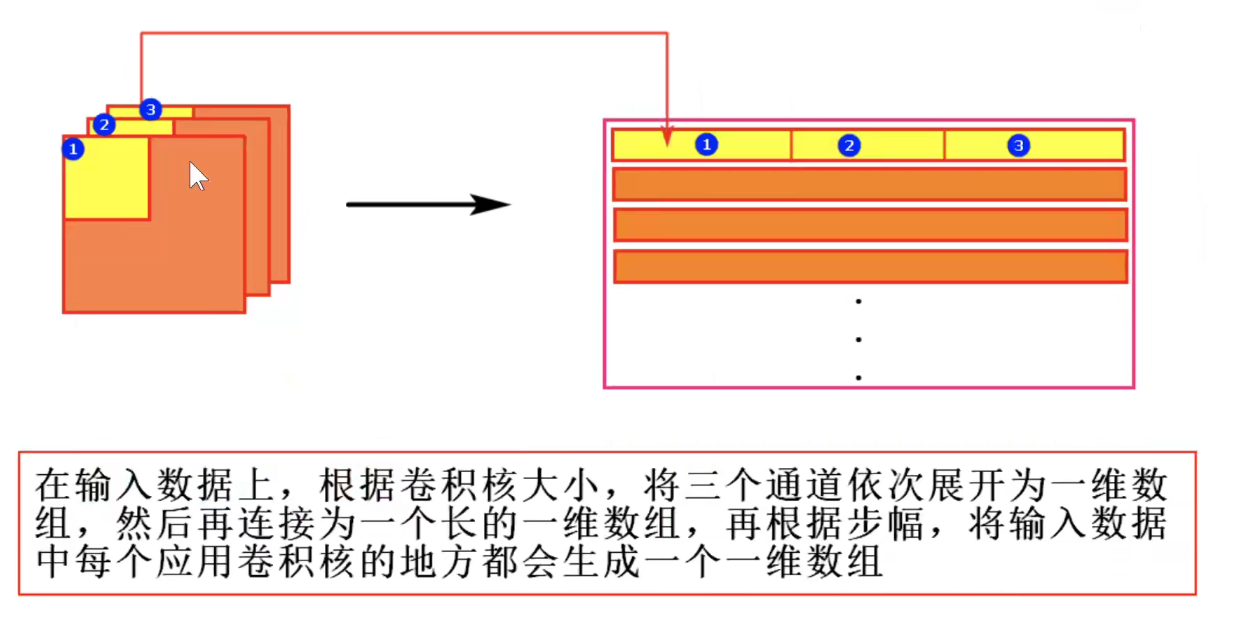
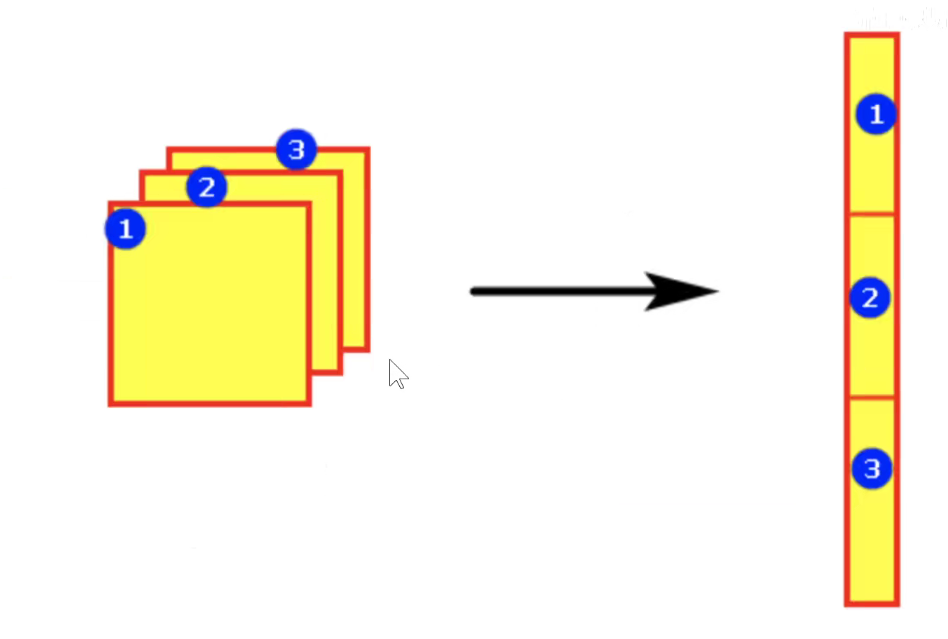
如下图所示:把每一个感受野拉成列向量。
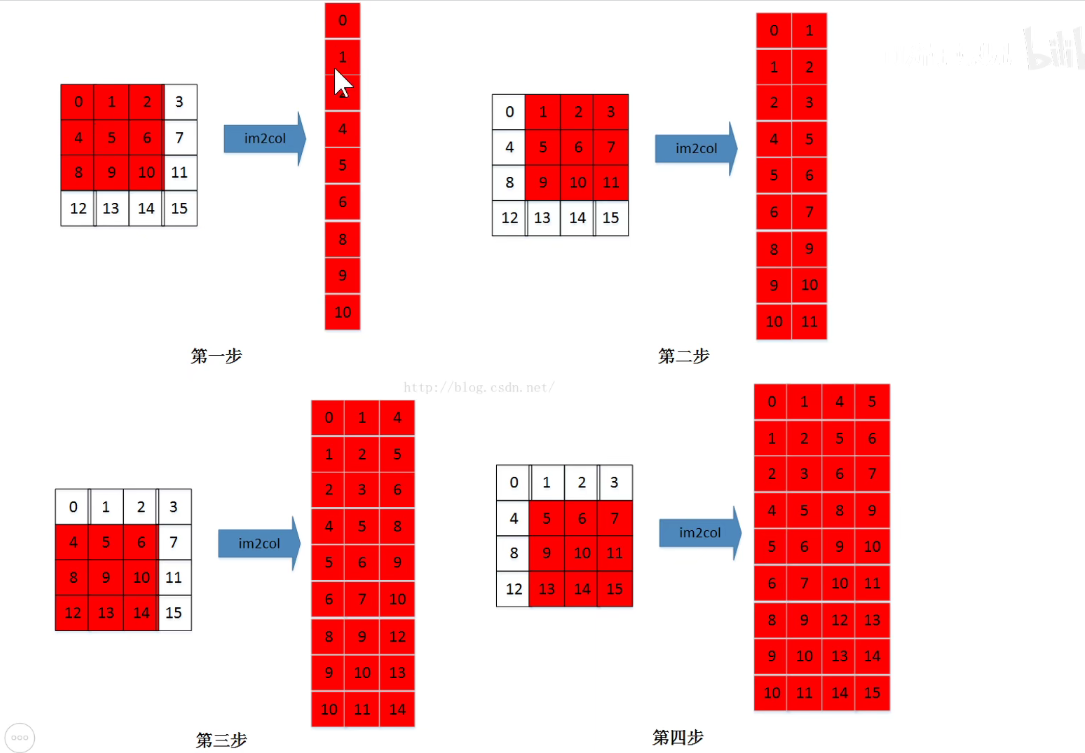
多通道图像如下所示:分别进行拉伸
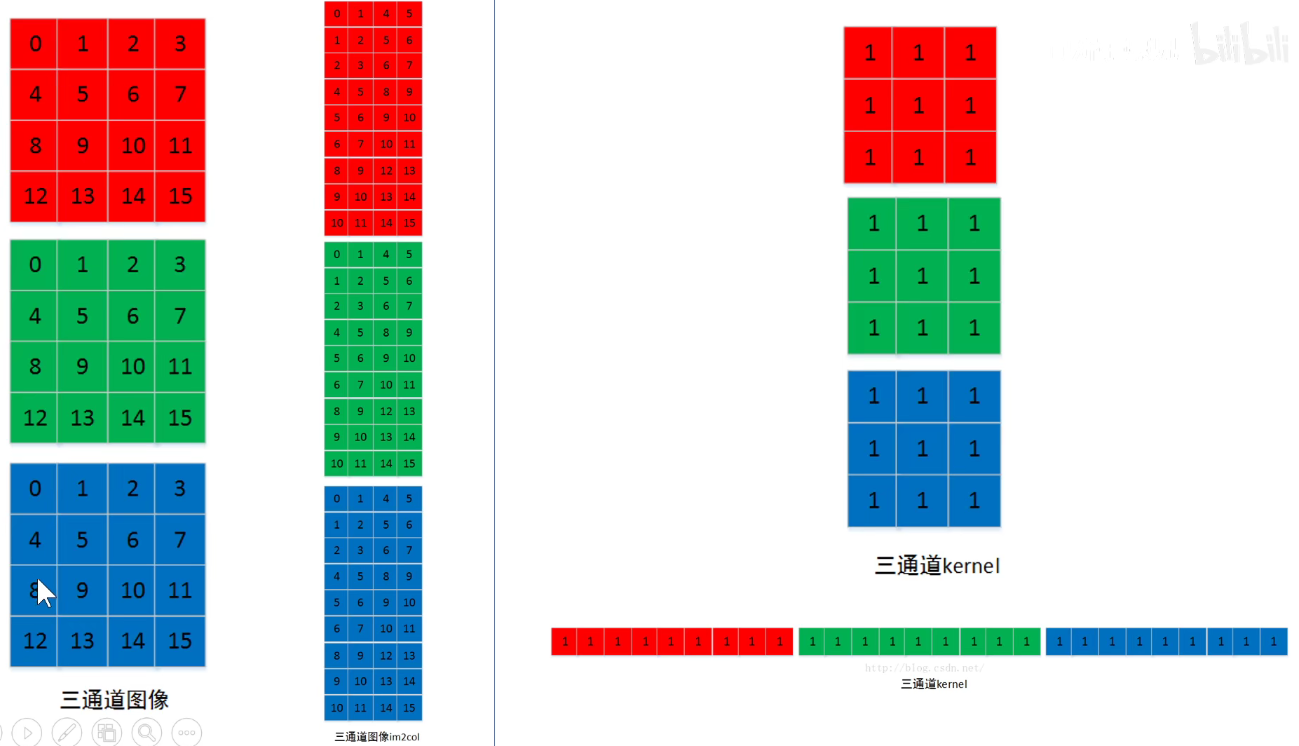
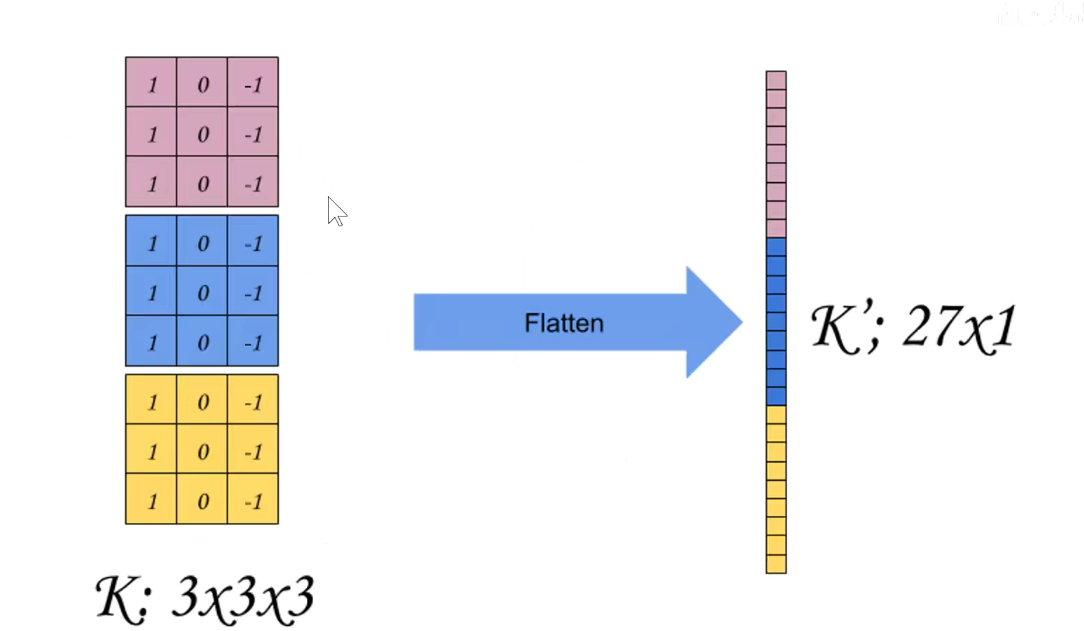
如下图所示:卷积核拉成的行向量 x 感受野拉成的列向量,再把结果还原回该有的维度,这表示可以把卷积运算变成矩阵的乘法运算。
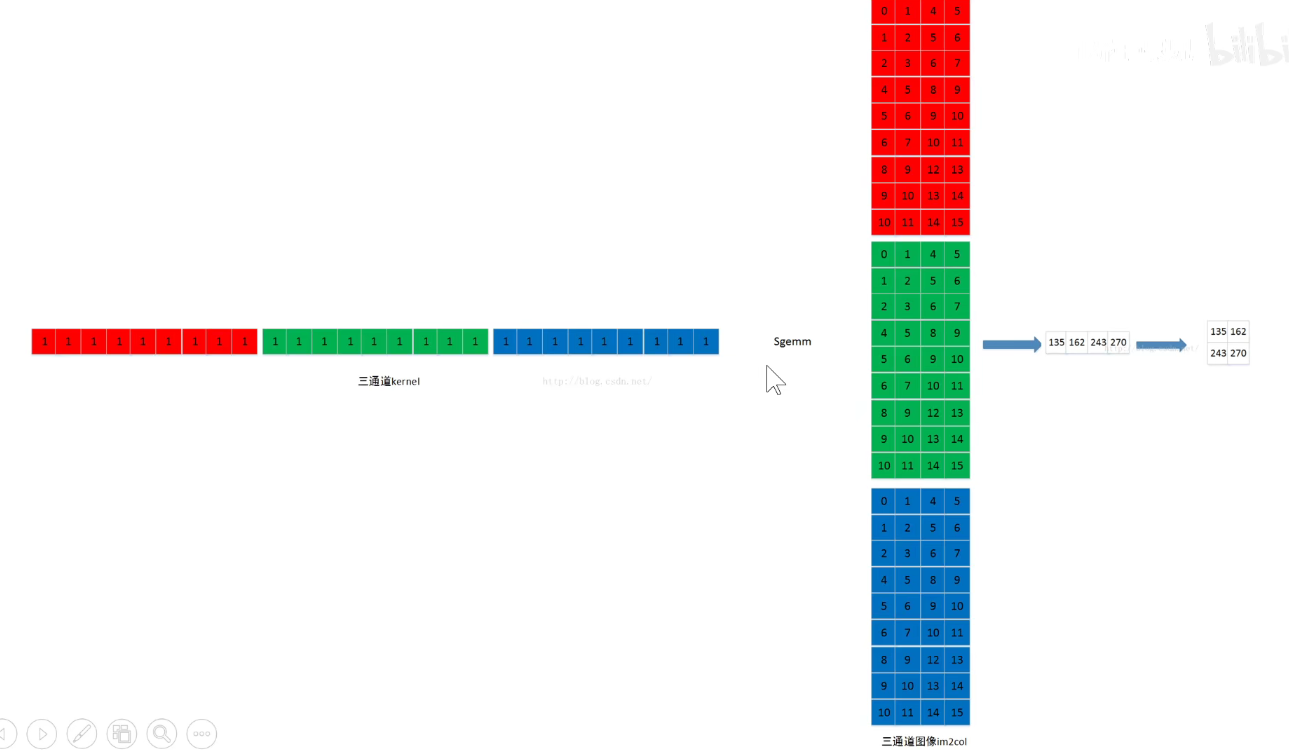
如果是三通道,则各自进行运算。再把三通道图像还原到他们该有的维度。
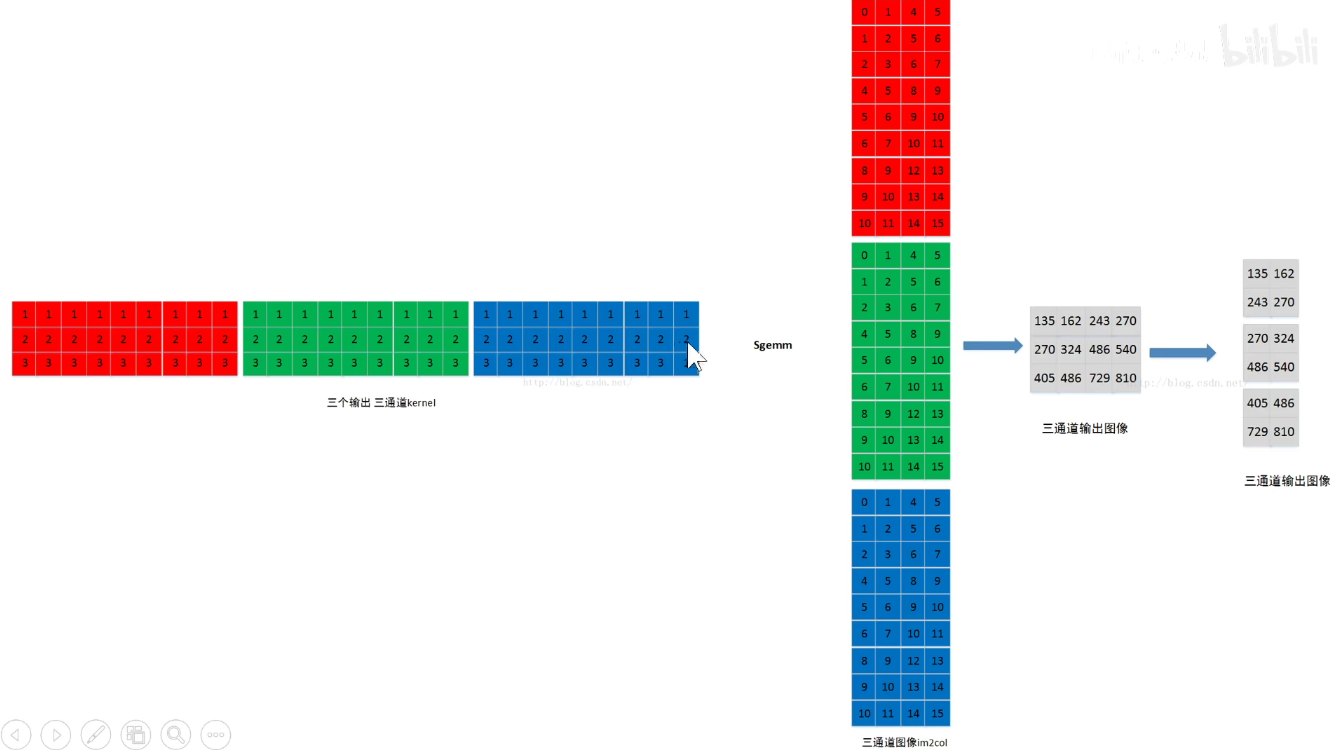
如下图:棋盘离散的变换操作,其实是一样的。
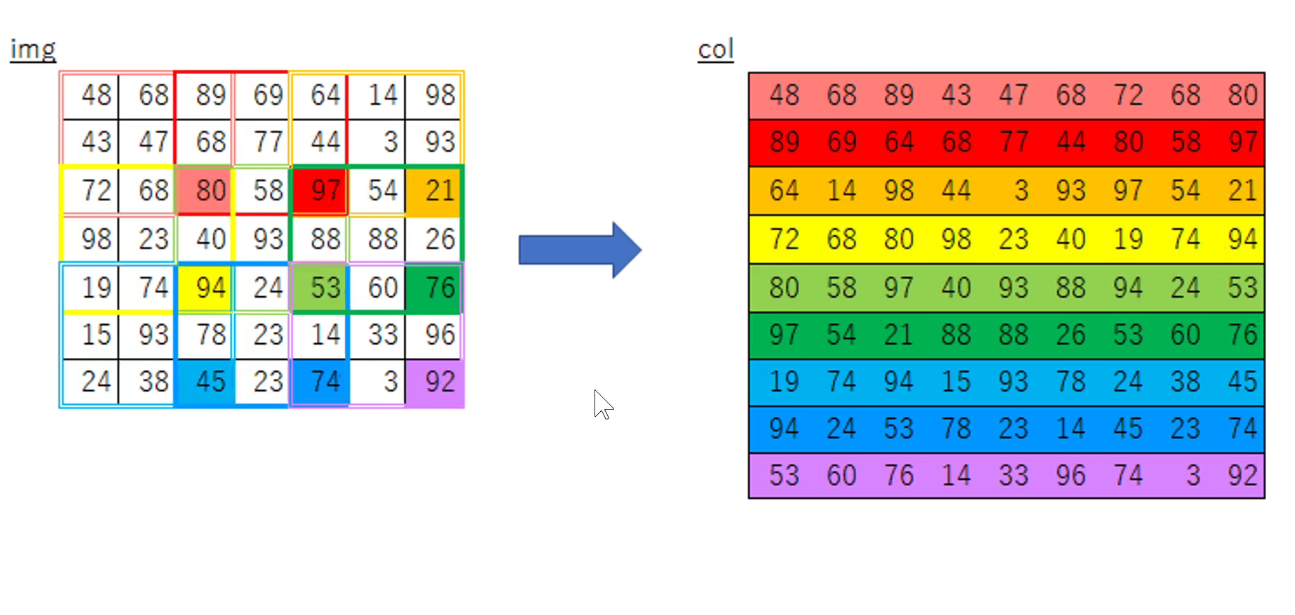
如下图:Caffe早期版本使用了im2col: Caffe作者贾扬清亲自回答了这个问题-https://www.zhihu.com/question/28385679


Caffe内部操作细节:如下图,左边的需要写很多for循环,让滑动窗口在原始图像上滑动,对应位置相乘求和,效率极低。右边的是im2col,变成矩阵的乘法,一口气可以算出结果。之前讲的是把卷积核拉成行向量,感受野拉成列向量,此处是把卷积核拉成列向量,感受野拉成行向量,道理是一样的。
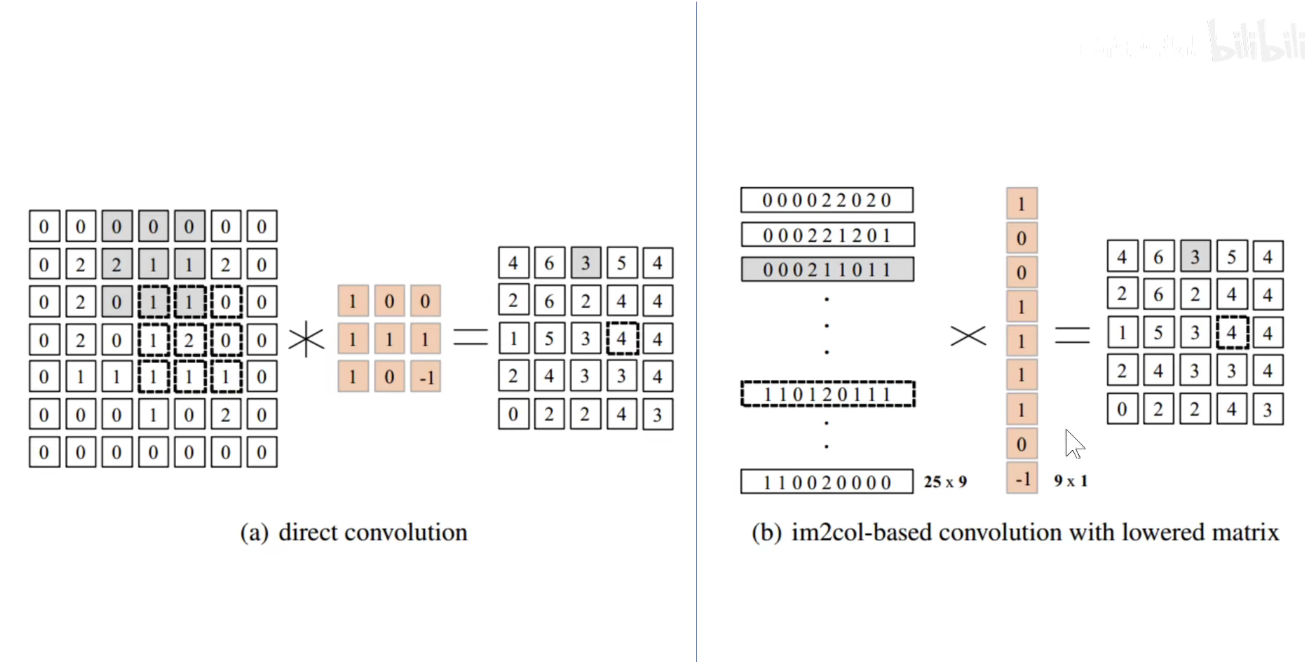
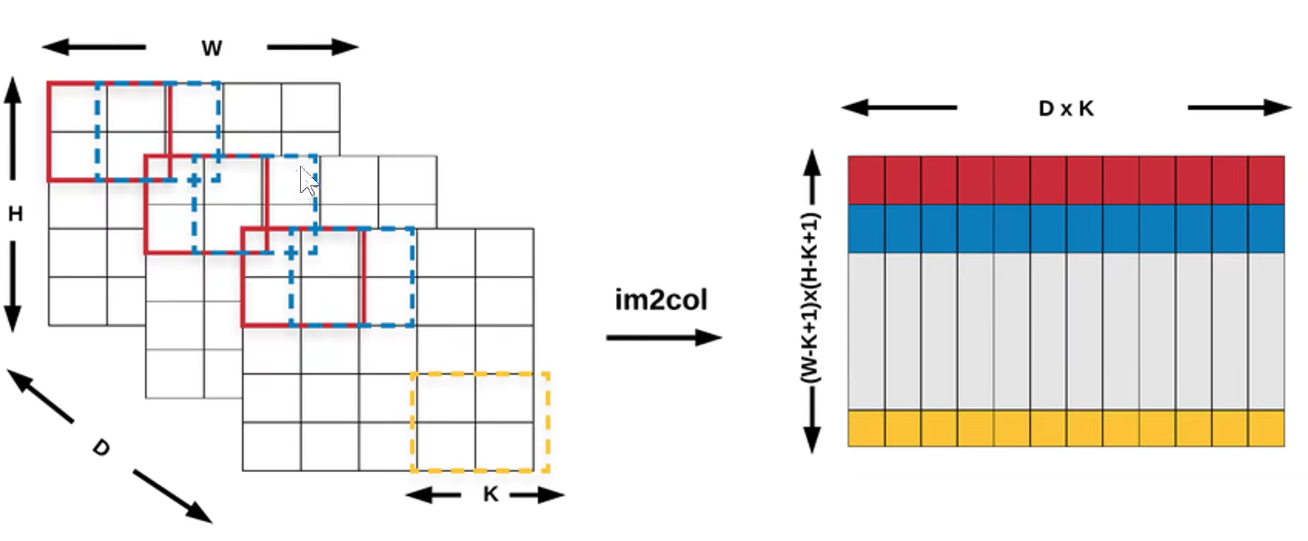
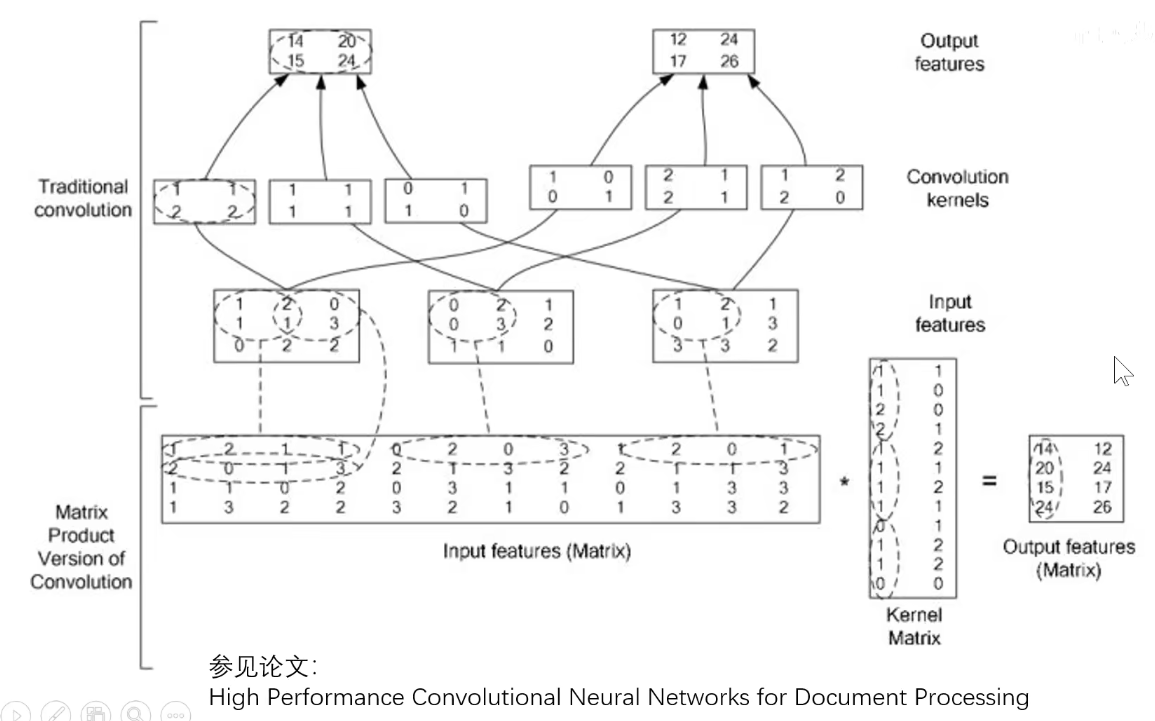
如下图是一篇论文专门将高效的卷积操作:中间是输入,中间以上是传统的小窗口,中间以下的是感受野变成行向量,卷积核变成列向量。
3.2 FFT-快速傅里叶变换

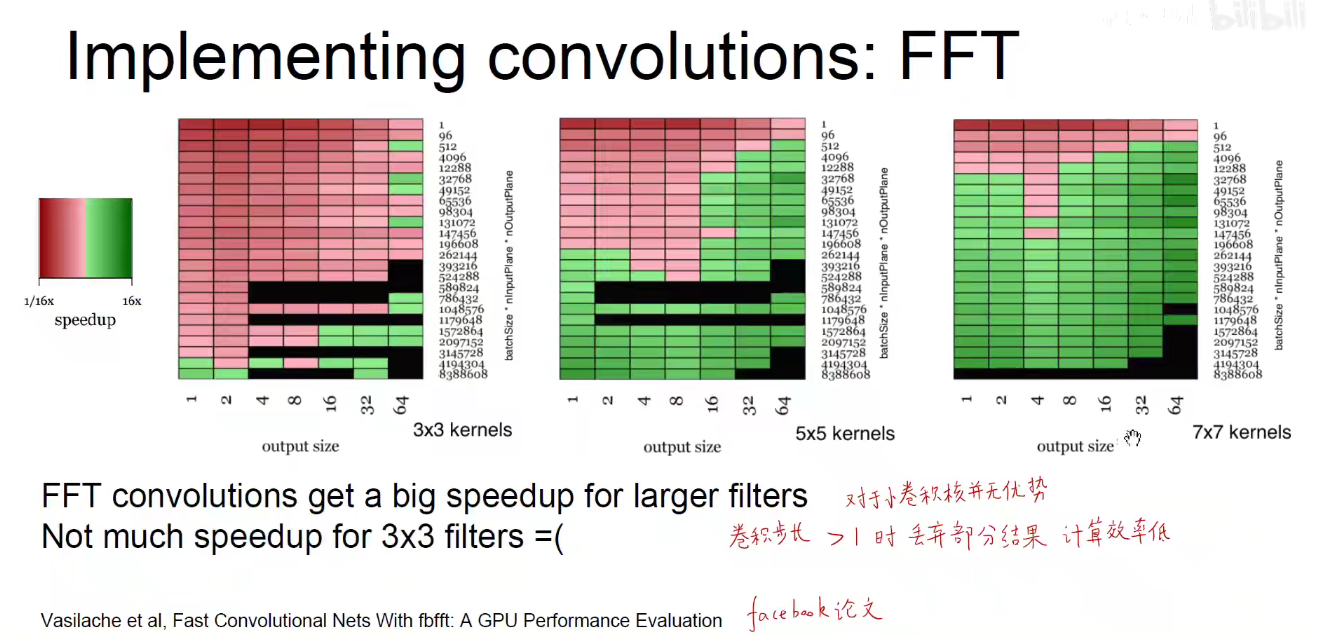
傅里叶变换:任何信号都可以由一系列不同频率不同幅度的正弦信号叠加而成。
时域信号通过傅里叶变换变成频域信号
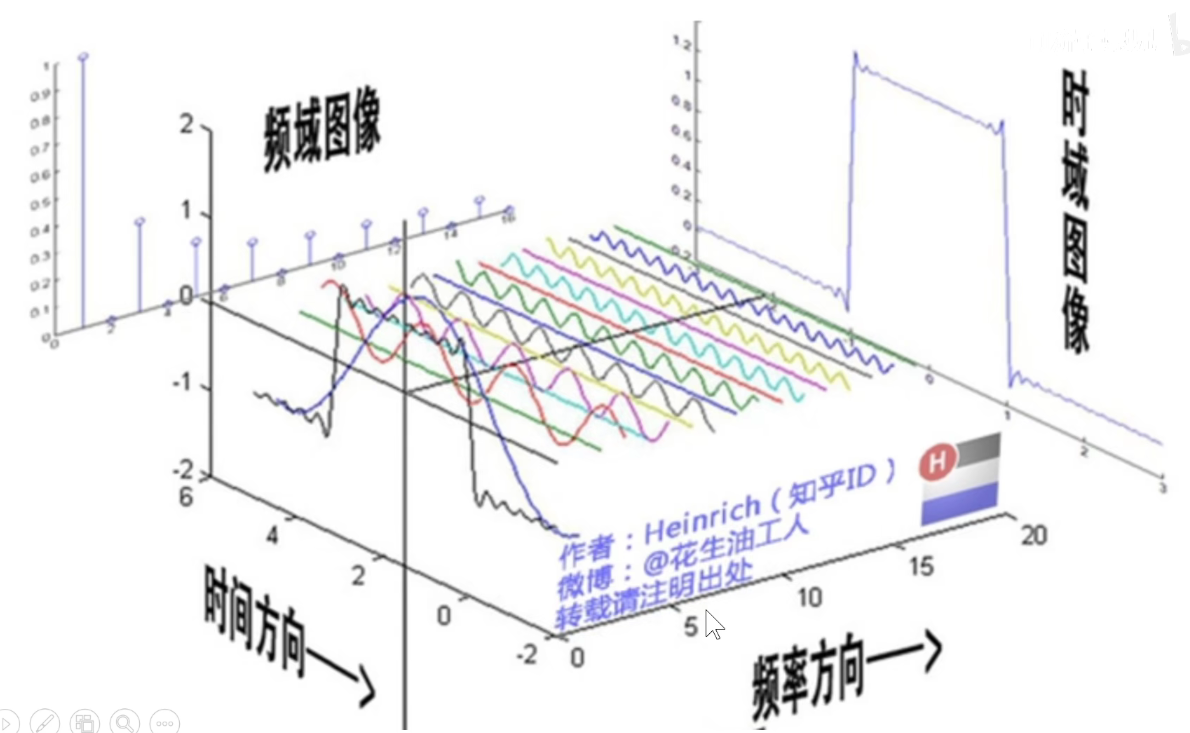
时域卷积=频域相乘

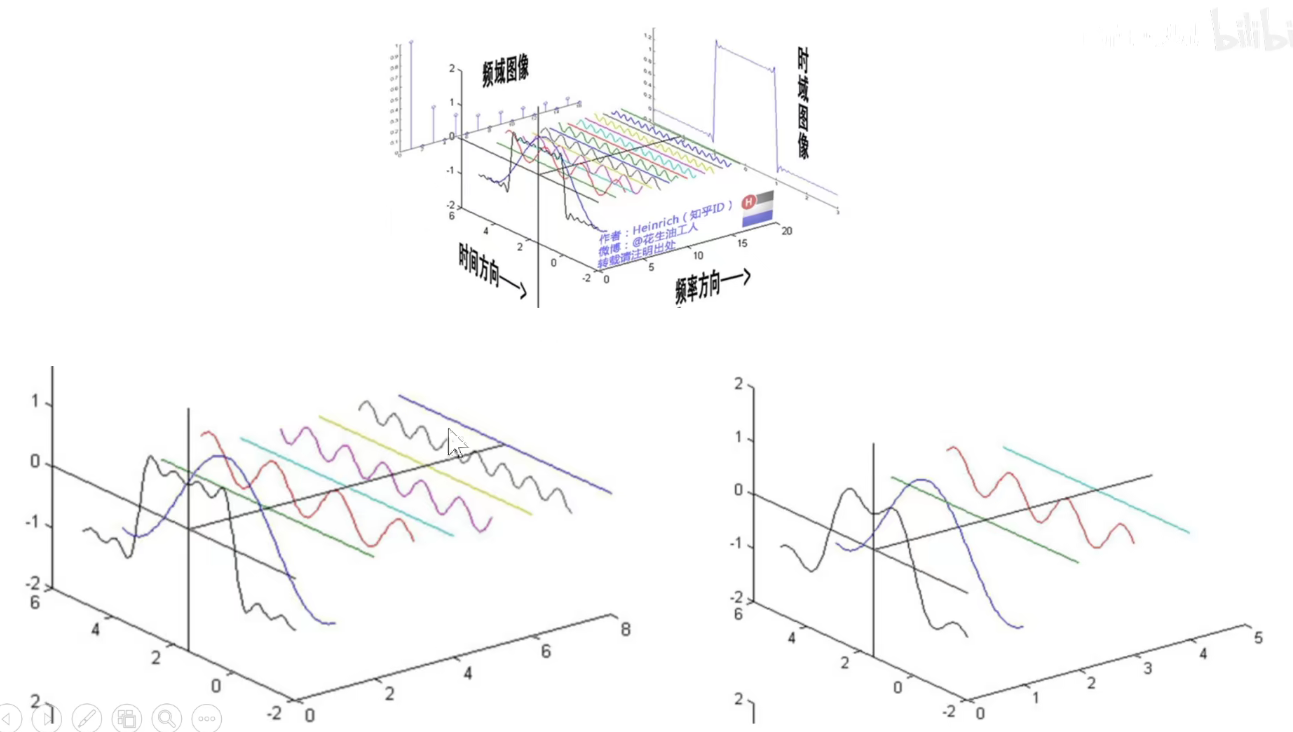
在图像上,明暗变化比较剧烈的地方就是高频区域。
卷积核本质上是二维信号滤波器。
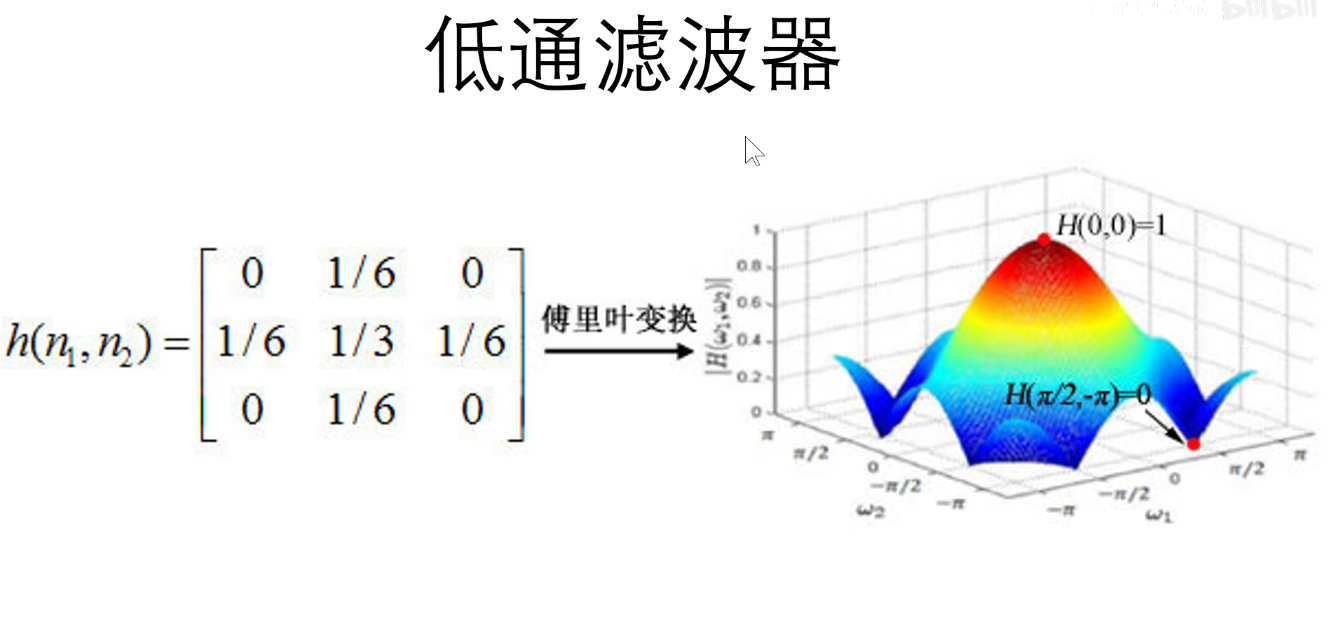
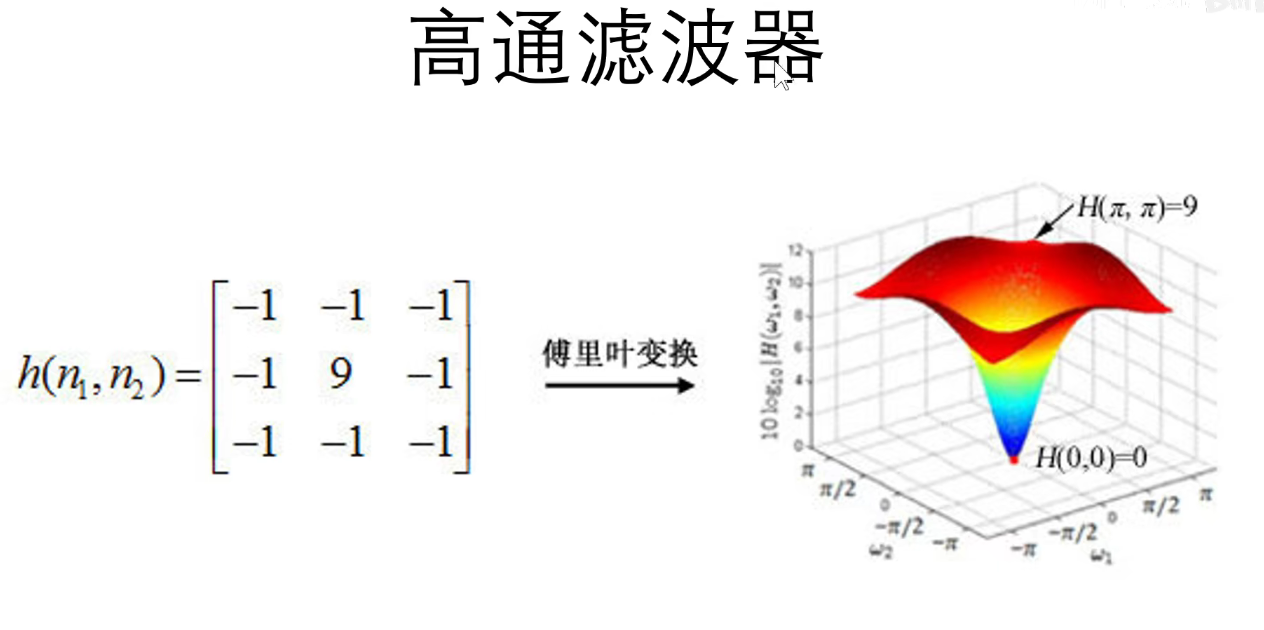
索贝尔算子:边缘检测

信号处理角度理解卷积操作:
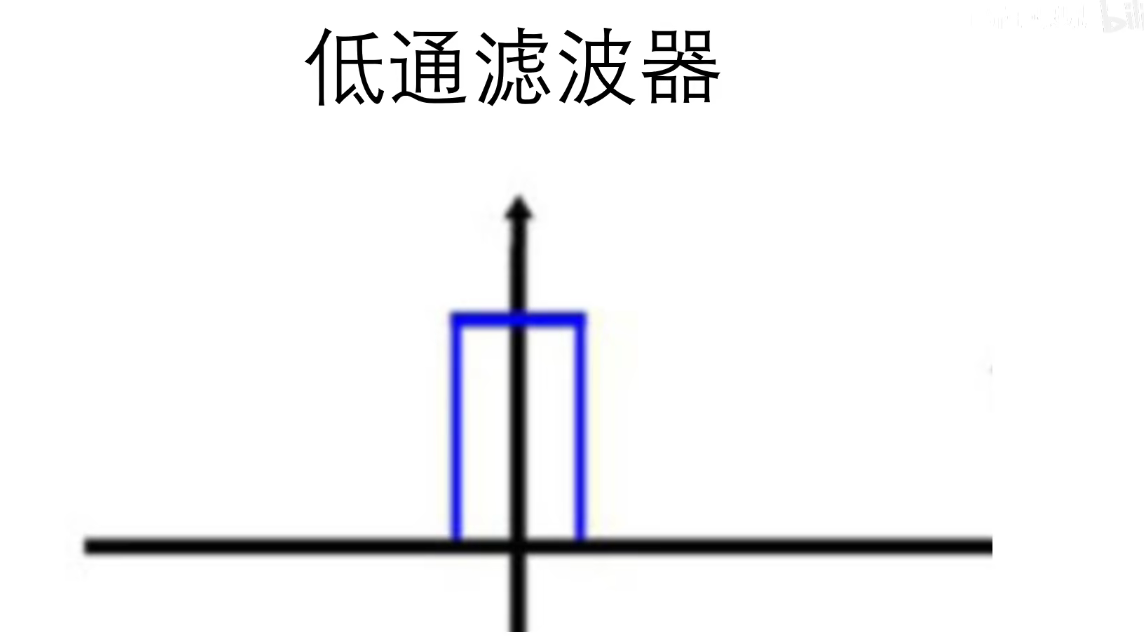
低通滤波器:允许低频信号通过,对图像进行了平滑和模糊。
高通滤波器:允许高频信号通过,图像的边缘一般是高频信号,对图像进行了锐化处理。



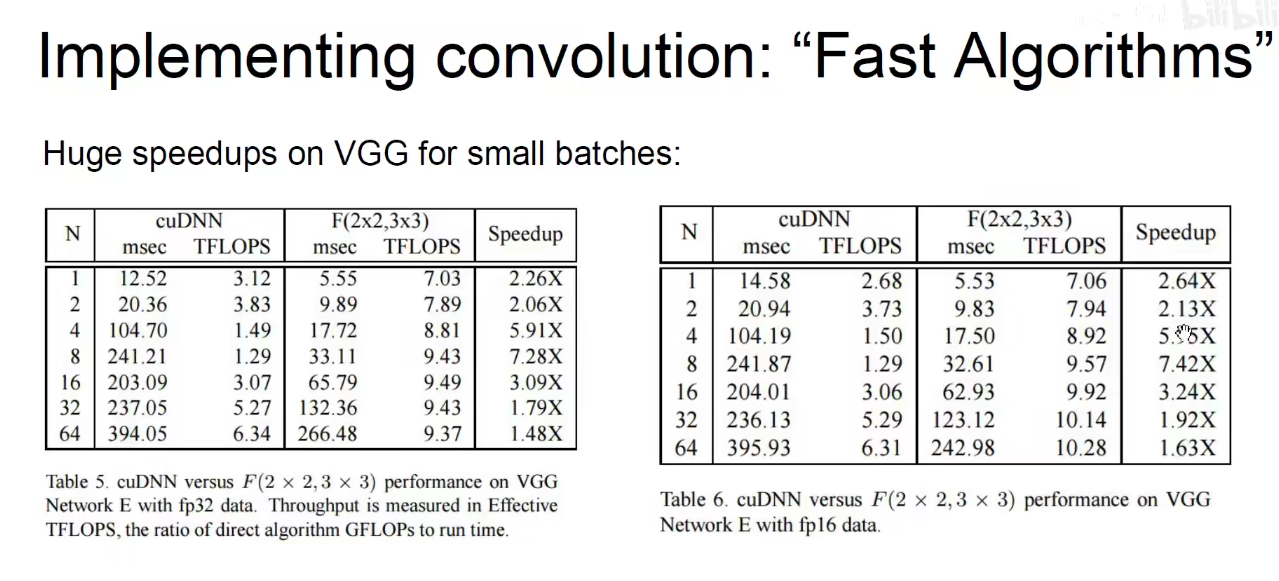
对于Strassen算法,效率如下图所示:
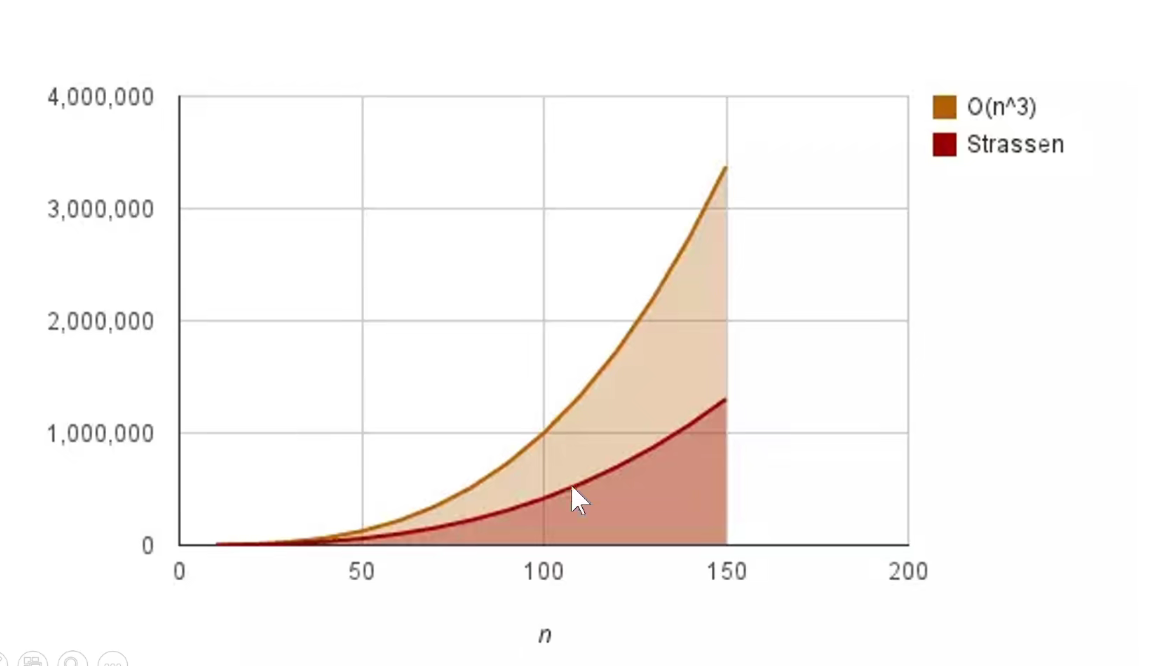
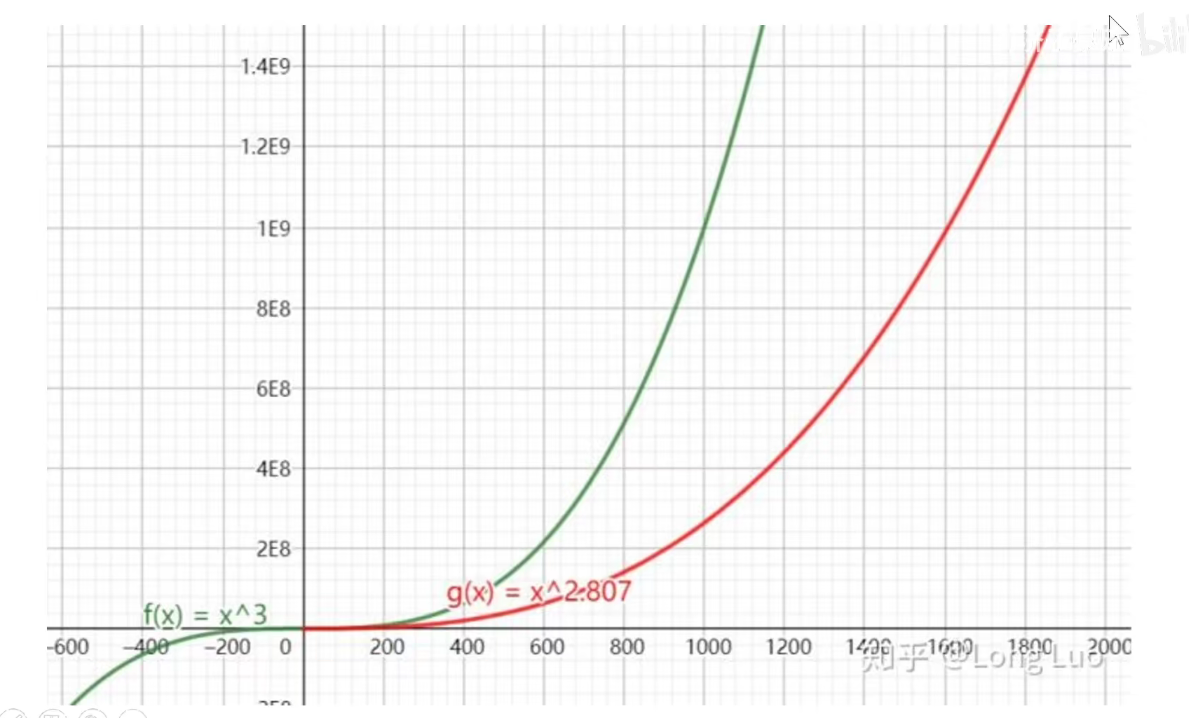

4 总结
