王喆《深度学习推荐系统》
1. 写在前面
最近整理推荐系统模型的时候, 第二个模型打算整理一下隐语义模型, 这里面绕不开一种思想就是矩阵分解, 而作为矩阵分解的经典方法SVD感觉这次有必要学学了, SVD不仅是一个数学问题,在工程应用中的很多地方都有它的身影,比如我之前在【白话机器学习篇】说到了PCA, 那是一种经典的降维方式, 而SVD同样的也可以用于降维, 并且掌握了SVD原理后再去看PCA那是相当简单的,在推荐系统方面,SVD更是名声大噪,在2006年, Koren将它应用于推荐系统并获得了Netflix大奖, 因此在推荐系统中也就出来了隐语义模型(Latent Factor Model)或者叫矩阵分解模型(Matrix Fatcorization), 它们的核心思想是通过寻找隐含特征来联系用户兴趣和商品,说白了其实就是把协同过滤里面的共现矩阵分解成了两个矩阵相乘的方式。 这个在具体整理的时候再谈, 总之, 这里面绕不开的一个名词就是SVD, 尽管数学上的这种SVD矩阵分解由于它对矩阵稠密的要求和计算复杂度大不太直接用于协同过滤里面的共现矩阵,但是源思想没变, 所以在这里先整理一下SVD的原理, 防止在整理矩阵分解模型的时候遇到SVD, RSVD, ASVD, SVD++等各种名词的时候一脸懵逼哈哈。
这篇文章是基本看着一篇博客整理过来的, 只是对里面的错别字和公式进行了改版, 对里面说的不太清晰的地方简单的补充了一下, 所以并不是完全原创文章, 注明一下原文章出处:https://blog.csdn.net/zhongkejingwang/article/details/43053513, 下面就是这个链接的原文了。
用SVD可以很容易得到任意矩阵的满秩分解,用满秩分解可以对数据做压缩。可以用SVD来证明对任意M × N M\times NM×N的矩阵均存在如下分解:
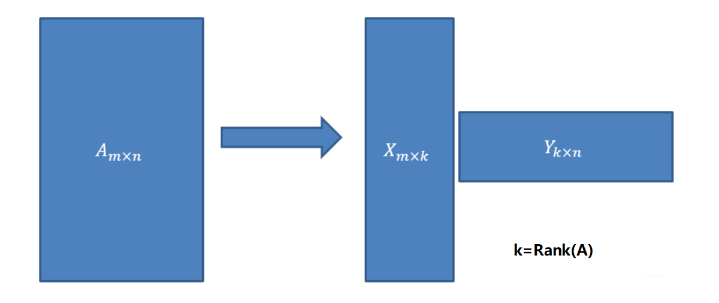
这个可以应用在数据降维压缩上!在数据相关性特别大的情况下存储X和Y矩阵比存储A矩阵占用空间更小!在开始讲解SVD之前,先补充一点矩阵代数的相关知识。
2. 正交矩阵
正交矩阵是在欧几里得空间里的叫法,在酉空间里叫酉矩阵,一个正交矩阵对应的变换叫正交变换,这个变换的特点是不改变向量的尺寸和向量间的夹角,那么它到底是个什么样的变换呢?看下面这张图
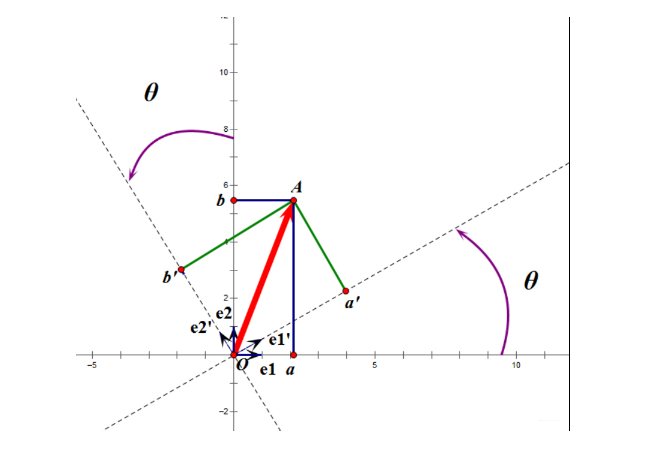
假设二维空间中的一个向量OA,它在标准坐标系也即e1、e2表示的坐标是中表示为(a,b)’(用’表示转置),现在把它用另一组坐标e1’、e2’表示为(a’,b’)’,存在矩阵U使得(a’,b’)’=U(a,b)’,则U即为正交矩阵。


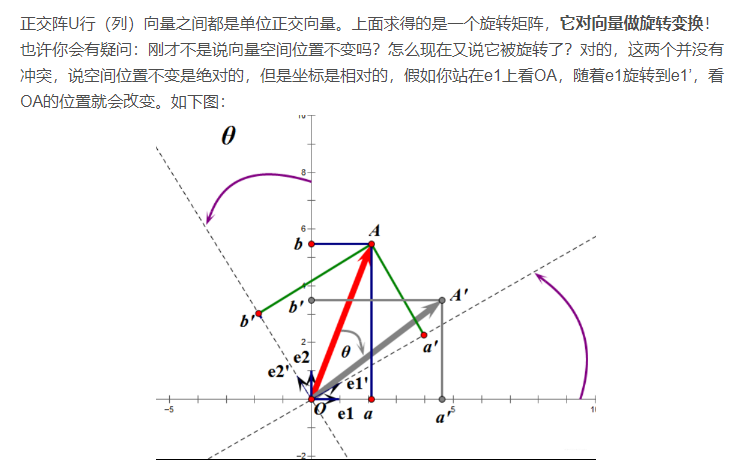
如图,如果我选择了e1’、e2’作为新的标准坐标系,那么在新坐标系中OA(原标准坐标系的表示)就变成了OA’,这样看来就好像坐标系不动,把OA往顺时针方向旋转了“θ”角度,这个操作实现起来很简单:将变换后的向量坐标仍然表示在当前坐标系中。
旋转变换是正交变换的一个方面,这个挺有用的,比如在开发中需要实现某种旋转效果,直接可以用旋转变换实现。正交变换的另一个方面是反射变换,也即e1’的方向与图中方向相反,这个不再讨论。
总结:正交矩阵的行(列)向量都是两两正交的单位向量,正交矩阵对应的变换为正交变换,它有两种表现:旋转和反射。正交矩阵将标准正交基映射为标准正交基(即图中从e1、e2到e1’、e2’)
3. 特征值分解—EVD



紧接着,在新的坐标系表示下,由中间那个对角矩阵对新的向量坐标换,其结果就是将向量往各个轴方向拉伸或压缩:
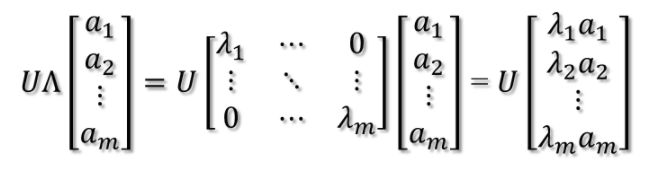
从上图可以看到,如果A不是满秩的话,那么就是说对角阵的对角线上元素存在0,这时候就会导致维度退化, 这样就可以降维了看没看到,这样就会使映射后的向量落入m维空间的子空间中。
最后一个变换就是U对拉伸或压缩后的向量做变换,由于U和U’是互为逆矩阵,所以U变换是U’变换的逆变换。
因此,从对称阵的分解对应的映射分解来分析一个矩阵的变换特点是非常直观的。假设对称阵特征值全为1那么显然它就是单位阵,如果对称阵的特征值有个别是0其他全是1,那么它就是一个正交投影矩阵,它将m维向量投影到它的列空间中。
根据对称阵A的特征向量,如果A是2*2的,那么就可以在二维平面中找到这样一个矩形,是的这个矩形经过A变换后还是矩形:
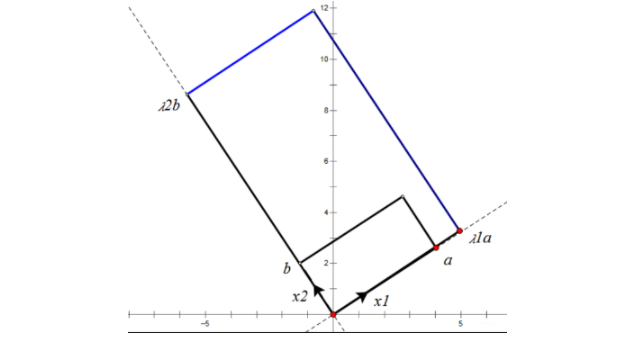
这个矩形的选择就是让其边都落在A的特征向量方向上,如果选择其他矩形的话变换后的图形就不是矩形了!
3. 奇异值分解—SVD
上面的特征值分解的A矩阵是对称阵,根据EVD可以找到一个(超)矩形使得变换后还是(超)矩形,也即A可以将一组正交基映射到另一组正交基!这个意思其实就是上面向量x的那三次变换, 开始的正交基假设的是A个特征向量。 而A变换之后, 又变回到了那组正交基上, 只不过是长度上发生了拉伸或者压缩, 方向没变。可以看那两个矩形。
那么现在来分析:对任意M*N的矩阵,能否找到一组正交基使得经过它变换后还是正交基?答案是肯定的,它就是SVD分解的精髓所在。SVD想做的这个变化不限于是上面的m*m的满秩对称矩阵A, 而是任意的A矩阵。
现在假设存在M*N矩阵A,事实上,A矩阵将n维空间中的向量映射到k(k<=m)维空间中, k=Rank(A)。现在的目标就是:在n维空间中找一组正交基,使得经过A变换后还是正交的。假设已经找到这样一组正交基:




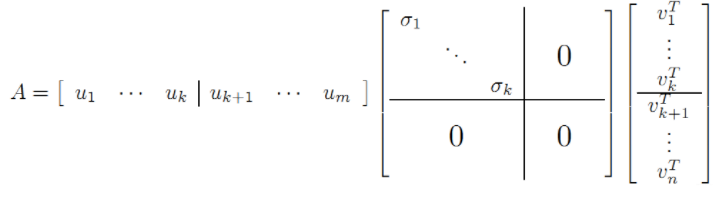
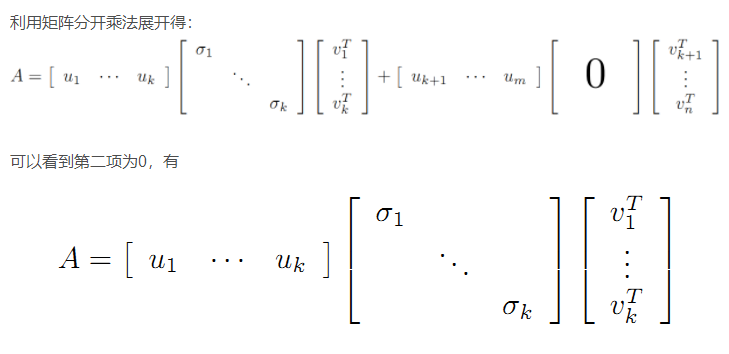
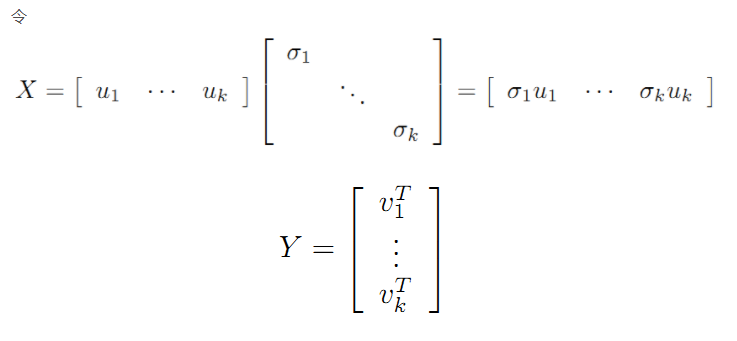
则A=XY即是A的满秩分解。
参考: