梯度下降算法的细节补充（凸函数，导数，偏导数，梯度，方向导数以及负梯度下降最快背后的泰勒身影）

2022-07-28

字数统计: 2.2k字 | 阅读时长: 7分

× 文章目录

1. 1. 写在前面
2. 2. 概念的简单介绍
3. 3. 负梯度方向下降最快的原因
4. 4. 几种常见的梯度下降法

王喆《深度学习推荐系统》

1. 写在前面

这篇文章，再来对梯度下降算法进行一个小的回顾，梯度下降算法是求解无约束多元函数极值最常用的数值方法，很多机器学习常用算法和神经网络都是以它作为算法框架进行优化参数。所以这个算法非常重要。

这篇文章会有两大部分组成，第一部分是一些概念的介绍，第二部分是一个说法背后的原因，围绕着下面的两张Photos进行一些细节的补充：

这张Photos里面提到了几个概念，第一个就是凸函数的概念，第二个是导函数的概念，第二个是梯度的概念，当然再加一个方向导数的概念作为第一部分，也就是概念方面的介绍。第二张Photo在说为啥梯度下降方法会有效:

这两张图片里面都提到了一个说法负梯度方向是f (x) 减小最快的方向，可是我们有想过这是为啥吗？这背后竟然会有泰勒的身影，所以第二部分就来看看这个问题，简单推导一下为啥是负梯度方向。

大纲如下

概念简单介绍
负梯度方向下降最快的原因
几种常见的梯度下降法

2. 概念的简单介绍

2.1 凸函数

在第一张图片中，我们看到了一些概念，这里进行简单的回归，第一个就是凸函数，之前看到一个公式： AI问题 = 模型 + 优化。任何一个优化问题（参数求解过程），都可以写成如下的形式：

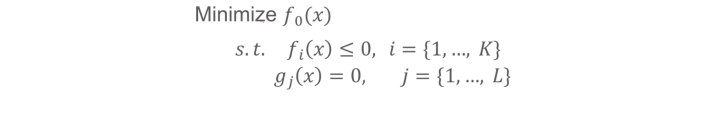
这个东西在统计学习方法的公式推导中，可是非常常见的，很多机器学习模型都是先有个目标函数，然后下面加一些约束，基于这些构造拉格朗日函数，然后试图去求参数，再涉及到稍微复杂一些的还会把拉格朗日函数的形式转换一下等，当然这里面往往也是会要求函数f₀(x)要是一个凸函数，满足KKT条件等，才能进行求解。

那么，什么样的函数是凸函数呢？在介绍凸函数之前，得先了解一个概念叫做凸集\

这是在说啥呢？其实，就是假如我们有一个很大的集合，在里面任意找两个点，只要在这两点之间的连线上的所有点都在这个集合里面，那么这个集合就是凸集。比如

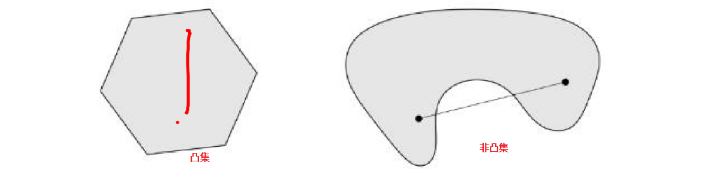
当然，两个凸集的交集也会是凸集，凸集的例子非常常见。有了凸集之后，我们就可以定义凸函数了：

这个就是凸函数的定义，这个公式说的啥意思呢？

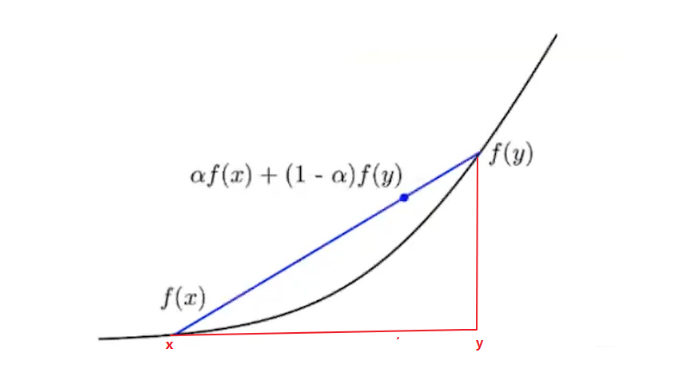
上面是凸函数的定义，下面给出两个证明函数是凸函数的定理：

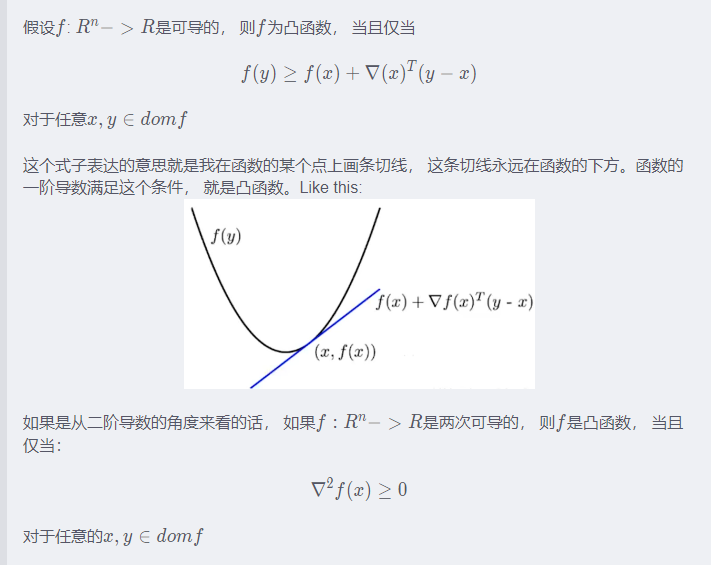
线性回归函数是凸函数，故这个就可以使用梯度下降法进行参数的更新。有了凸函数的概念，我们基于这个再看看导数。

2.2 导数与偏导数

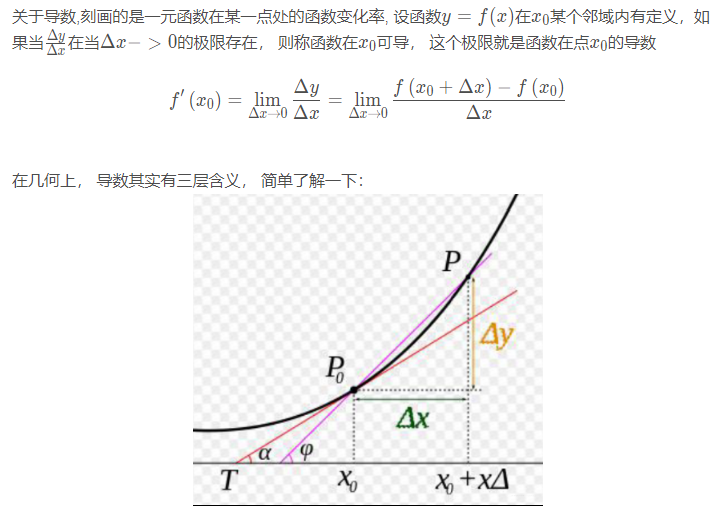
2.3 方向导数

定义导数、偏导数、方向导数都是说如果说某条件下极限存在，导数的本质是极限及代表函数的变化率，偏导数反映的是函数沿坐标轴方向的变化率，有所限制，所以引入方向导数表示沿任意一方向的变化率。

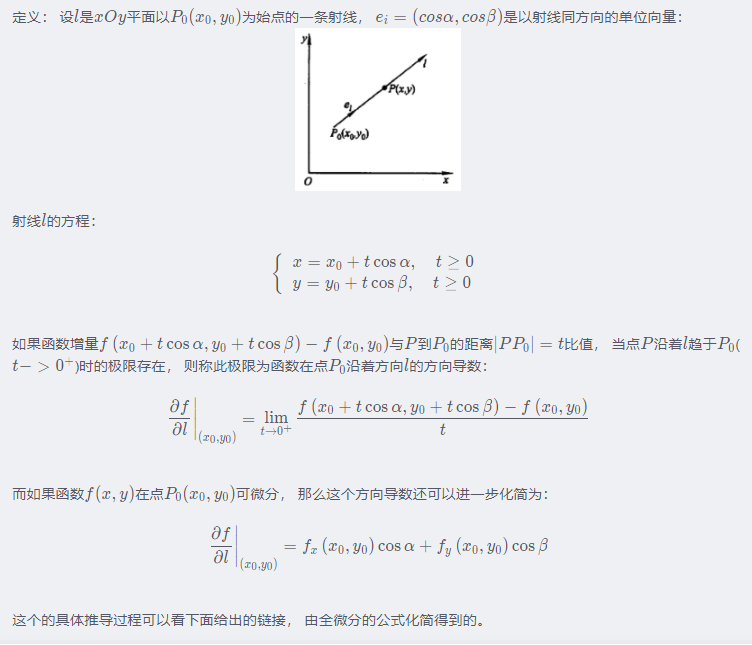
上面这是方向导数， 注意方向导数的本质是个数值，可能现在有些懵逼了，讲这些概念到底在说啥，不是梯度下降嘛？还差一个梯度的概念，就能把这一串知识串起来了。

2.4 梯度

在平面上确定某一点可能存在无数个方向导数，我们怎样找到其中一个方向导数来描述函数最大变化率？

由梯度的定义可以发现，梯度的方向是确定的，如果点P PP的坐标确定，那么梯度的大小也会确定。那么根据上面方向导数的那个公式，就可以再进一步化简：

所以可以用沿梯度方向的方向导数来描述是函数最大变化率，即梯度方向是函数变化率最大的方向，在梯度定义的时候就已经赋予了它这个特性。但是，为什么会有这样的一个特性呢？

下面我们来简单的推导一下。

3. 负梯度方向下降最快的原因

4. 几种常见的梯度下降法

明白了梯度下降算法的原理，下面补充几种常见的梯度下降算法，主要是

批梯度下降（Batch Gradient Descent, BGD）
Mini-batch梯度下降（Mini-batch Gradient Descent, MBGD）
随机梯度下降（Stochastic Gradient Descent, SGD）

4.1 批梯度下降法

批量梯度下降法（Batch Gradient Descent，简称BGD）是梯度下降法最原始的形式，它的具体思路是在更新每一参数时都使用所有的样本来进行更新，也就是方程中的m表示样本的所有个数。更新公式如下：

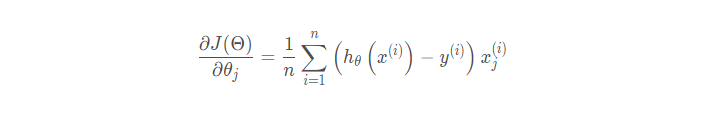
这里可以清楚地看到，批量梯度下降法计算梯度时，使用全部样本数据，分别计算梯度后除以样本个数（取平均）作为一次迭代使用的梯度向量。伪代码：

1
2
3

for i in range(max_iters):
    grad = evaluate_gradient(loss_functiion, data, initial_params)
    params = params - learning_rate * grad

优点：全局最优解；易于并行实现
缺点：样本数目很多时，训练过程会很慢

4.2 随机梯度下降法

由于批梯度下降每跟新一个参数的时候，要用到所有的样本数，所以训练速度会随着样本数量的增加而变得非常缓慢。随机梯度下降正是为了解决这个办法而提出的。

它的具体思路是在更新每一参数时都使用一个样本来进行更新，也就是以上批处理方程中的n等于1。每一次跟新参数都用一个随机选择的样本，更新很多次。如果样本量很大的情况（例如几十万），那么可能只用其中几万条或者几千条的样本，就已经将theta迭代到最优解了，对比上面的批量梯度下降，迭代一次需要用到十几万训练样本，一次迭代不可能最优，如果迭代10次的话就需要遍历训练样本10次，这种更新方式计算复杂度太高。但是，SGD伴随的一个问题是噪音较BGD要多，使得SGD并不是每次迭代都向着整体最优化方向。更新方式如下：

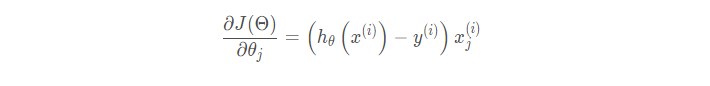
for i in range(max_iters):
    np.random.shuffle(data)
    for sample in data:
        grad = evaluate_gradient(loss_functiion, sample, initial_params)
        params = params - learning_rate * grad

优点：训练速度快
缺点：准确度下降，并不是每一步全局最优，不易于并行实现

4.3 小批量梯度下降

我们从上面两种梯度下降法可以看出，其各自均有优缺点，那么能不能在两种方法的性能之间取得一个折衷呢？即，算法的训练过程比较快，而且也要保证最终参数训练的准确率，而这正是小批量梯度下降法（Mini-batch Gradient Descent，简称MBGD）的初衷。

小批量梯度下降法（Mini-batch Gradient Descent，简称MBGD）：它的具体思路是在更新每一参数时都使用一部分样本来进行更新，也就是批处理方程中的n的值大于1小于所有样本的数量。为了克服上面两种方法的缺点，又同时兼顾两种方法的优点。

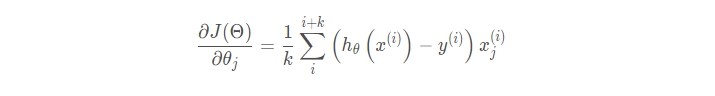
小批量梯度下降法使用一部份样本数据（上式中为k个）参与计算，既降低了计算复杂度，又保证了解的收敛性。

for i in range(max_iters):
    np.random.shuffle(data)
    for batch in get batches(data, batch_size=50):
        grad = evaluate_gradient(loss_functiion, batch, initial_params)
        params = params - learning_rate * grad

4.4 三种方法比较

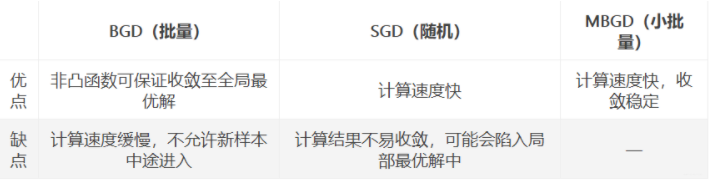
如果样本量比较小，采用批量梯度下降算法。如果样本太大，或者在线算法，使用随机梯度下降算法。在实际的一般情况下，采用小批量梯度下降算法。

参考