王喆《深度学习推荐系统》
文章出处:https://blog.csdn.net/wuzhongqiang/article/details/108471107
1. 写在前面
今天是梯度提升树GBDT的理论学习和细节补充, 之前整理过XGBOOST和Lightgbm, 在那里面提到了GBDT, 但是只是简单的一过, 并没有关注太多GBDT的细节, 所以这次借着整理推荐系统里面的GBDT+LR模型的机会, 重新过了一遍GBDT和LR的基础知识, 确实发现忽略了很多知识, 而GBDT和逻辑回归模型都是作为面试考核的大点, 所以有必要细一些了。
关于逻辑回归的细节, 在这篇文章中进行了补充, 今天的重点是GBDT, GBDT全称梯度提升决策树,在传统机器学习算法里面是对真实分布拟合的最好的几种算法之一,在前几年深度学习还没有大行其道之前,gbdt在各种竞赛是大放异彩。原因大概有几个,一是效果确实挺不错。二是即可以用于分类也可以用于回归。三是可以筛选特征。这三点实在是太吸引人了,导致在面试的时候大家也非常喜欢问这个算法, 下面就从算法的原理与公式推导, 算法如何选择特征, 如何进行回归和分类等几方面进行一个整理。
PS: 这个算法非常重要, 现在机器学习算法最常用的XGBOOST, Lightgbm, catboost这几大巨头算法都是基于这个算法的基础上进行发展起来的, 面试里面一般会问到的关于这个算法的问题, 大致有下面几个, 由于我也刚开始接触细节部分, 先整理其中的几个, 后面再慢慢加:
- gbdt算法的流程?
- gbdt如何选择特征?
- gbdt如何构建特征?
- gbdt如何用于分类
- gbdt 通过什么方式减少误差 ?
- gbdt的效果相比于传统的LR,SVM效果为什么好一些 ?
- gbdt 如何加速训练?
- gbdt的参数有哪些,如何调参 ?
- gbdt 实战当中遇到的一些问题 ?
- gbdt的优缺点 ?
大纲如下:
- GBDT? 我们先从提升树(BDT)开始吧
- 梯度提升之GBDT的原理(上面问题的1, 2)
- 从梯度下降的角度再看GBDT,会有一个新的感受(GBDT的残差为啥可以用负梯度近似?)
- GBDT如何构建特征(3)
- GBDT如何进行分类(4)
- 为何GBDT受人青睐(6, 10)
Ok let’s go!
2. GBDT? 先从提升树开始
在介绍GBDT之前, 先简单的介绍一下BDT, 也就是Boosting Decision Tree, 这是以CART决策树为基学习器的集成学习方法, 关于集成学习, 这里就不过多赘述了, 可以参考白话机器学习算法理论+实战之AdaBoost算法。 提升树模型可以表示为决策树的加法模型:
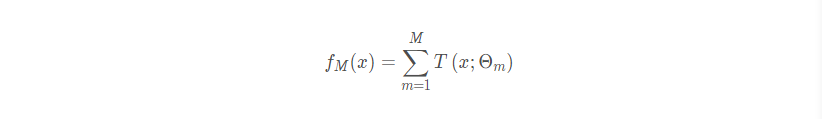

这里的L() 是损失函数,回归算法选择的损失函数一般是均方差(最小二乘)或者绝对值误差;而在分类算法中一般的损失函数选择对数函数来表示。 这是李航老师《统计学习方法》里面的原内容, 也是对提升树比较好的总结。
如果对上面的公式一脸懵逼, 那么我们拿一个图来看一下BDT的一个学习流程, 然后再回顾一下上面的这些公式, 就会有一种豁然开朗的感觉(初极狭, 才通人, 复行数十步, 豁然开朗哈哈)
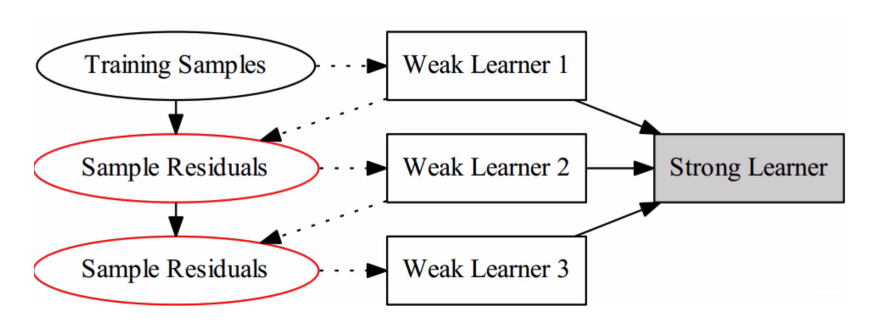
根据这个图先梳理一遍BDT的流程:
boosting方法之前已经提到过, 是由多个弱学习器进行组合得到的一个强学习器, 而每个弱学习器之间是相互关联的, AdaBoost是boosting家族的一员, 它与BDT不同, AdaBoost中弱学习器之间的关联关系是前一轮学习器表现不行的样本, 而GBDT中弱学习器之间的关联是残差。
给我一些训练样本, 我们先训练第一个弱学习器, BDT里面的话就是决策树了, 关于决策树的问题这里依然不多说, 可以参考白话机器学习算法理论+实战之决策树, 训练完了第一个学习器, 就可以对样本进行一个预测, 此时会得到一个与真实标签的一个残差, 那么就可以用这个残差来训练后面的学习器, 也就是第二个分类器关注于与前面学习器与真实标签的差距, 这样依次类推, 最后会得到n个弱分类器。 那么我这n个分类器进行加和, 就得到了最终的学习器。最后就是用这个东西进行预测。 关于这个拟合残差的这部分, 在白话机器学习算法理论+实战番外篇之Xgboost做了比较详细的赘述, 这里就不再重复了, 因为这篇文章内容也很多, 不要再冗余了哈哈。
根据上面的这个简单过程, 我们再来理解一下《统计学习方法》里面的公式, 提升树实际上是加法模型和前向分布算法, 表示为:



关于回归问题的提升树算法, 李航老师书上有个比较好的例子, 由于比较细致, 这里只摘一部分, 但是在摘之前, 需要先整理一下CART回归树的生成方式, 因为之前整理决策树全是分类任务, 而这次要整理的BDT或者是下面的GBDT都是用CART回归树作为的基分类器, 所以有必要了解一下CART回归树的生成过程, 这也对应着面试过程中的一个问题, 如何选择特征? 这个细节其实就是CART回归树的生成过程, 因为CART回归树生成的过程就是一个特征选择的过程。(这里PS一下:gbdt的弱分类器默认选择的是CART TREE。其实也可以选择其他弱分类器的,选择的前提是低方差和高偏差, Boosting就是干降低偏差这个事情的。框架服从boosting 框架即可)

然后寻找最优切分点j 和最优切分点s 。 这个是关键, 如何寻找?
具体的求解
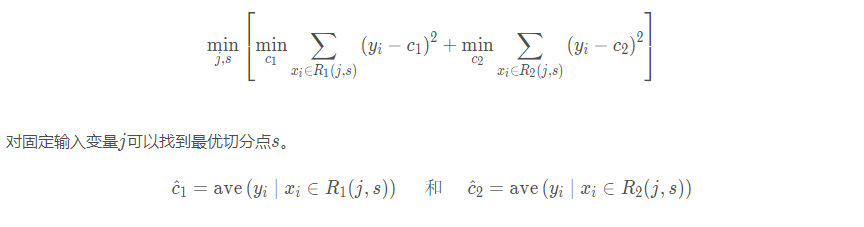
遍历所有输入变量, 找到最优切分变量j, 构成一个对(j,s)。 依此将输入空间划分为两个区域。 重复上面的过程, 直到满足条件, 这样就生成了一棵回归树。
如果感觉上面的内容比较头大, 那么可以看下面的这个例子, 这个例子既说明了一下回归树是如何生成的, 又解释了回归问题提升树的原理, 这是李航老师书上的一个例子:


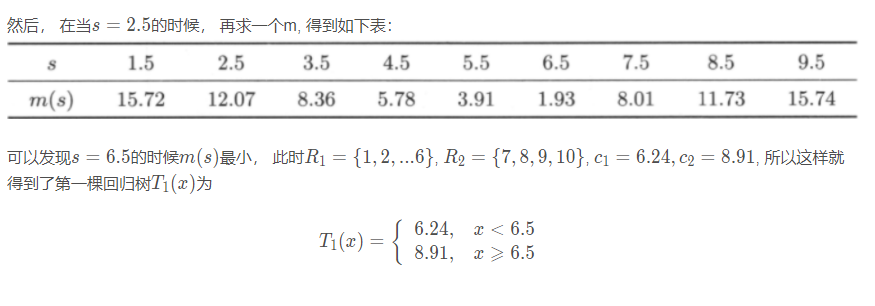


3. 梯度提升之GBDT的原理
提升树利用加法模型和前向分布算法实现学习的优化过程, 但损失函数是平方损失或者指数损失时, 优化比较简单, 但是对于一般的损失函数而言, 往往每一步优化不容易, 针对这个问题, 所以Friedman大神提出了利用最速下降的近似方法, 即利用损失函数的负梯度来拟合基学习器。就是它了

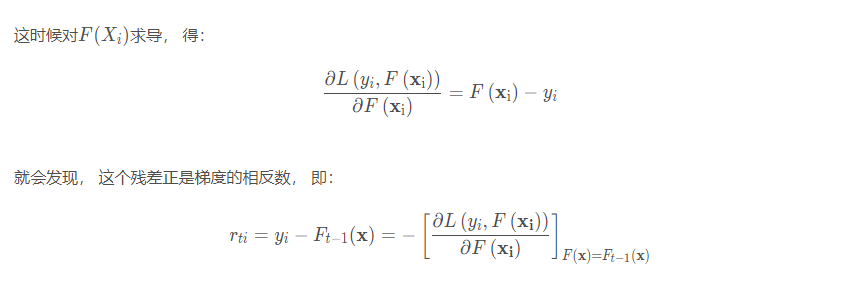
所以在GBDT中使用负梯度作为残差进行拟合, 当然这是平方损失函数, 其他损失的话, 也会得到近似的结论, 只不过不是完全相等, 这里放张图体会一下:

这其实就是GBDT的核心了, 即利用损失函数的负梯度作为回归问题提升树算法中的残差的近似值去拟合一个回归树。gbdt 每轮迭代的时候,都去拟合损失函数在当前模型下的负梯度。这样每轮训练的时候都能够让损失函数尽可能快的减小,尽快的收敛达到局部最优解或者全局最优解。
下面就是GBDT的梯度提升流程(这里是宏观的角度, 即分类器是个大类), 和BDT差不多,只不过残差这里直接用负梯度进行了替代。

如果公式不好看, 那就看图, 这个图应该也是了然:
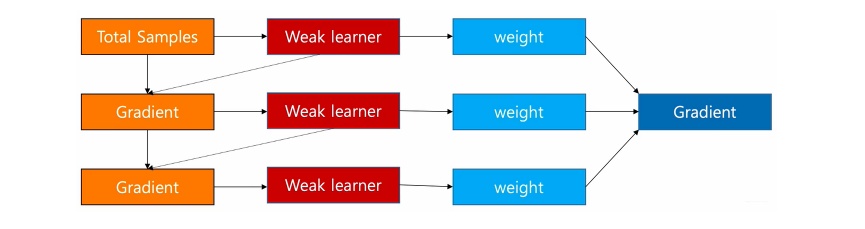
可以发现GBDT和提升树的区别是残差使用了损失函数的负梯度来替代, 且每个基学习器有了对应的参数权重。gbdt通过多轮迭代,每轮迭代产生一个弱分类器,每个分类器在上一轮分类器的残差基础上进行训练。对弱分类器的要求一般是足够简单,并且是低方差和高偏差的(因为训练的过程是通过降低偏差来不断提高最终分类器的精度)。 弱分类器一般会选择为CART TREE(也就是分类回归树)。由于上述高偏差和简单的要求每个分类回归树的深度不会很深。最终的总分类器是将每轮训练得到的弱分类器加权求和得到的(也就是加法模型)。
这就是GBDT的训练流程了, 当然要明确一点, gbdt无论用于分类还是回归一直都是使用CART回归树, 这个原因后面会说, 既然是用的回归树, 我们就有:
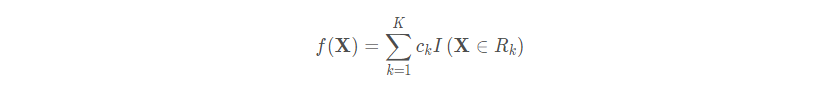
这时候, 流程可以化成下面的形式了,



4. 从梯度下降的角度再看GBDT,会有一个新的感受
这个是我上面产生了这个问题之后,又重新查的相关资料得到的所悟, 具体细节可以看上面的链接, 这里我们从梯度下降的角度再去看GBDT。
GBDT叫做梯度提升树, 这和梯度下降有啥联系吗? 我最下边也从百面机器学习上摘抄了下两者的区别,简单的来说就是一个是在函数空间,一个是在参数空间,而GBDT的求解过程就可以理解为梯度下降在函数空间的优化过程。
那么,下面就可以进行类比了, 首先, 在梯度下降里面,我们是可以通过一阶泰勒展开来证明负梯度方向是目标函数下降最快的方向,具体的可以看我之前的博文总结。这里写结论:






这样,就回到了XGBoost的本质上去了,是不是也不是那么神秘了哈哈,XGBoost更像是牛顿法在函数空间的求解过程。当然,目前这是我自己的发现哈,没有找到任何参考。
5. GBDT如何构建特征
其实说gbdt能够构建特征并非很准确,gbdt 本身是不能产生特征的,但是我们可以利用gbdt去产生特征的组合。在CTR预估中,工业界一般会采用逻辑回归去进行处理,在逻辑回归那篇文章中已经说过,逻辑回归本身是适合处理线性可分的数据,如果我们想让逻辑回归处理非线性的数据,其中一种方式便是组合不同特征,增强逻辑回归对非线性分布的拟合能力。
长久以来,我们都是通过人工的先验知识或者实验来获得有效的组合特征,但是很多时候,使用人工经验知识来组合特征过于耗费人力,造成了机器学习当中一个很奇特的现象:有多少人工就有多少智能。关键是这样通过人工去组合特征并不一定能够提升模型的效果。所以我们的从业者或者学界一直都有一个趋势便是通过算法自动,高效的寻找到有效的特征组合。Facebook 在2014年 发表的一篇论文便是这种尝试下的产物,利用gbdt去产生有效的特征组合,以便用于逻辑回归的训练,提升模型最终的效果。
这本应该是推荐系统那边的模型, 后面会在那边再详细整理一下这个, 这里简单整理一下这个过程:看论文里面的这个图:
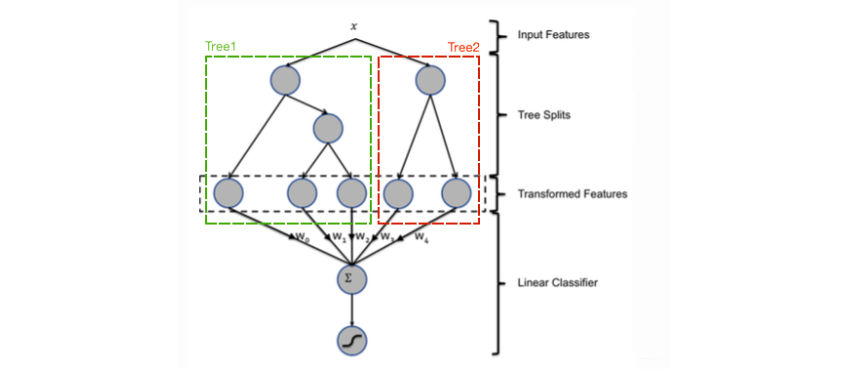
我们 使用 GBDT 生成了两棵树,两颗树一共有五个叶子节点。我们将样本 X 输入到两颗树当中去,样本X 落在了第一棵树的第二个叶子节点,第二颗树的第一个叶子节点,于是我们便可以依次构建一个五维的特征向量,每一个纬度代表了一个叶子节点,样本落在这个叶子节点上面的话那么值为1,没有落在该叶子节点的话,那么值为 0.
于是对于该样本,我们可以得到一个向量[0,1,0,1,0] 作为该样本的组合特征,和原来的特征一起输入到逻辑回归当中进行训练。实验证明这样会得到比较显著的效果提升。
关于这个模型的详细整理和代码实践部分, 可以参考推荐系统专栏里面的LR+GBDT模型, 这里不多说, 但是这里会有一个问题, 就是LR+GBDT模型一般是用于点击率预测里面, 而点击率预测是个典型的分类问题(点击或者不点击), 而我们上面一直说GBDT用的是CART回归树, 那么我们上面那部分进行样本类别划分的时候, 是怎么划分的呢? 回归树不是输出连续值吗? 我们怎么训练上面的GBDT模型?
所以下面才是重点, GBDT如何用于分类?
6. GBDT如何用于分类?
首先明确一点,gbdt 无论用于分类还是回归一直都是使用的CART 回归树。不会因为我们所选择的任务是分类任务就选用分类树,这里面的核心是因为gbdt 每轮的训练是在上一轮的训练的残差基础之上进行训练的。这里的残差就是当前模型的负梯度值 。这个要求每轮迭代的时候,弱分类器的输出的结果相减是有意义的。残差相减是有意义的。
如果选用的弱分类器是分类树,类别相减是没有意义的。上一轮输出的是样本 x 属于 A类,本一轮训练输出的是样本 x属于 B类。 A 和 B 很多时候甚至都没有比较的意义,A 类- B类是没有意义的。 那么我们如何进行分类呢?
假设样本X总共有K类, 来了一个样本, 我们使用gbdt来判断样本x属于哪一类? 流程如下:

如果感觉上面的理论比较难理解, 那么依然是来一个例子, 鸢尾花分类的数据集作为例子, 看一下gbdt多分类的过程。
数据集如下:
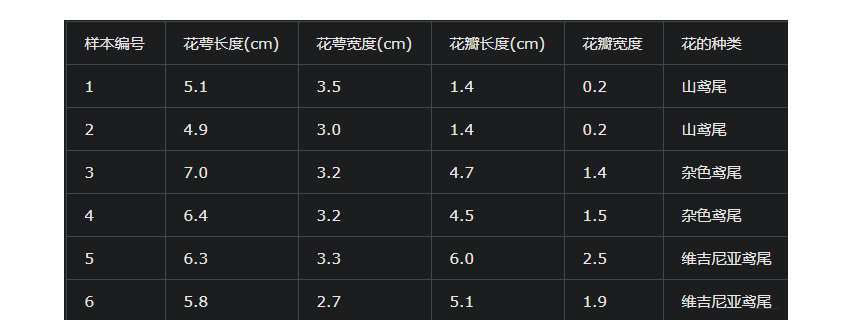
这是一个有6个样本的三分类问题。我们需要根据这个花的花萼长度,花萼宽度,花瓣长度,花瓣宽度来判断这个花属于山鸢尾,杂色鸢尾,还是维吉尼亚鸢尾。具体应用到gbdt多分类算法上面。我们用一个三维向量来标志样本的label。[1,0,0] 表示样本属于山鸢尾,[0,1,0] 表示样本属于杂色鸢尾,[0,0,1] 表示属于维吉尼亚鸢尾。
以样本1为例, 第一轮要训练3棵CART树, 对于第一棵CART回归树, 训练样本是[5.1, 3.5, 1.4, 0.2], label是1,第二棵 训练样本是[5.1, 3.5, 1.4, 0.2], label是0, 第三棵训练样本是[5.1, 3.5, 1.4, 0.2], label是0。
下面我们看CART 1是如何生成的, CART 1生成过程是从这四个特征中找一个特征作为CART 1的节点, 比如花萼长度作为节点, 6个样本当中花萼长度 大于5.1 cm的就是 A类,小于等于 5.1 cm 的是B类。生成的过程其实非常简单,但是有两个问题 :
- 是哪个特征最合适?
- 是这个特征的什么特征值作为切分点?
即使我们已经确定了花萼长度做为节点。花萼长度本身也有很多值。在这里我们的方式是遍历所有的可能性,找到一个最好的特征和它对应的最优特征值可以让当前式子的值最小。
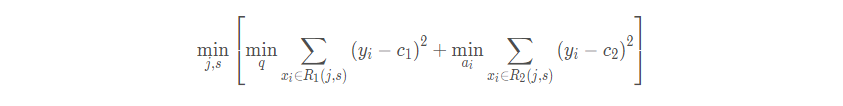
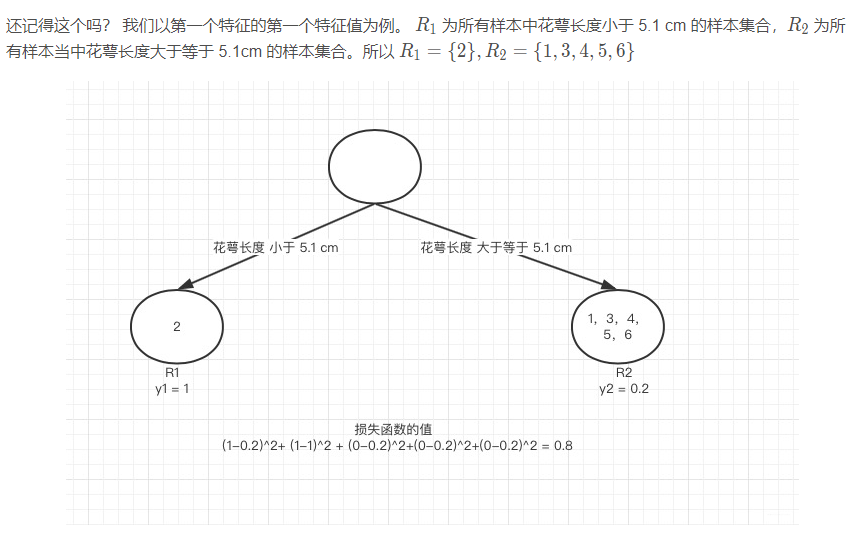
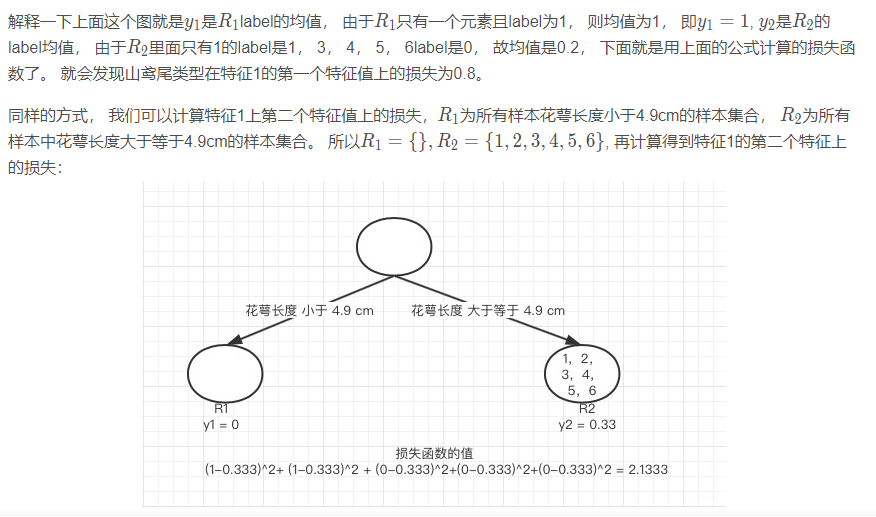
这样我们可以遍历所有特征的所有特征值,找到让这个式子最小的特征以及其对应的特征值。 在这里我们算出来让这个式子最小的特征花萼长度,特征值为5.1 cm。这个时候损失函数最小为 0.8。
于是我们的预测函数为:

类别2和类别3的也能算出来, 然后就可以得到残差, 每个样本都是如此, 就可以进行第二轮的训练了。
这就解决了上面的问题4, 最后再整理一个。
7. 为何GBDT如此受人青睐
GBDT的优势 首先得益于 Decision Tree 本身的一些良好特性,具体可以列举如下:
Decision Tree 可以很好的处理 missing feature,这是他的天然特性,因为决策树的每个节点只依赖一个 feature,如果某个 feature 不存在,这颗树依然可以拿来做决策,只是少一些路径。像逻辑回归,SVM 就没这个好处。
Decision Tree 可以很好的处理各种类型的 feature,也是天然特性,很好理解,同样逻辑回归和 SVM 没这样的天然特性。
对特征空间的 outlier 有鲁棒性,因为每个节点都是 x < 𝑇 的形式,至于大多少,小多少没有区别,outlier 不会有什么大的影响,同样逻辑回归和 SVM 没有这样的天然特性(SVM好像有,因为它只关注支持向量)。
如果有不相关的 feature,没什么干扰,如果数据中有不相关的 feature,顶多这个 feature 不出现在树的节点里。逻辑回归和 SVM 没有这样的天然特性(但是有相应的补救措施,比如逻辑回归里的 L1 正则化)。
数据规模影响不大,因为我们对弱分类器的要求不高,作为弱分类器的决策树的深 度一般设的比较小,即使是大数据量,也可以方便处理。像 SVM 这种数据规模大的时候训练会比较麻烦。
预测极端的计算速度快, 树与树之间可并行计算
采用决策树作为弱分类使得GBDT模型具有较好的可解释性和鲁棒性,能自动发现特征间的高阶关系,且不需要对数据进行特殊处理(如归一化)。
当然 Decision Tree 也不是毫无缺陷,通常在给定的不带噪音的问题上,他能达到的最佳分类效果还是不如 SVM,逻辑回归之类的。但是,我们实际面对的问题中,往往有很大的噪音,使得 Decision Tree 这个弱势就不那么明显了。而且,GBDT 通过不断的叠加组合多个小的 Decision Tree,他在不带噪音的问题上也能达到很好的分类效果。换句话说,通过GBDT训练组合多个小的 Decision Tree 往往要比一次性训练一个很大的 Decision Tree 的效果好很多。因此不能把 GBDT 理解为一颗大的决策树,几颗小树经过叠加后就不再是颗大树了,它比一颗大树更强。
局限性还是有的:
- GBDT在高维稀疏的数据集上, 表现不如支持向量机或者神经网络
- GBDT在处理文本分类特征问题上,相对其他模型的优势不如它在处理数值型特征时明显
- 训练过程需要串行训练,只能在决策树内部采用一些局部的手段提高训练速度
关于GBDT的理论和细节, 先到这里, 更详细的可以参考下面的第三个链接,这里就先不都整理过来了, 有了上面的GBDT的这些知识, 对于了解推荐系统里面的GBDT+LR模型, 或者GBDT+FM模型就比较轻松了, 对于了解XGBOOST和Lightgbm应该也会比较轻松了。
铺垫已经完成, 下一个就要一睹GBDT+LR模型的真容了 😉
参考:
李航老师 – 《统计学习方法》
西瓜书第八章 - 集成学习
这里依然是画几个重点
梯度提升和梯度下降的区别
GBDT使用梯度提升作为训练方法, 而逻辑回归或者神经网络在训练过程中往往采用的是梯度下降作为训练方法, 二者有什么区别吗或者联系吗?
同: 两者都是在每一轮的迭代中,利用损失函数相对于模型的负梯度方向的信息来对当前模型进行更新
异: 在梯度下降中,模型是以参数化形式表示, 从而模型的更新等价于参数的更新, 而在梯度提升中,模型并不需要进行参数化表示,而是直接定义在函数空间中,从而大大扩展了可以使用的模型种类。

GBDT在什么情况下比逻辑回归算法差?
高维稀疏的数据集,gbdt对维度超高的稀疏数据集,其正则项约束基本没用,并且决策空间会变成太多零散的决策小空间,具体可见上gbdt为何不好处理高基数类别特征的问题。
而lr的 l1 正则项可以很好的约束没啥用 的稀疏特征,直接w置0即可。
GBDT对输入数据有什么要求,如果效果比较差,可能是什么原因造成的?
如果训练集的效果很差,说明原始数据相对于gbdt算法来说实在太差了,特征基本没什么区分度,xgb这种拟合能力超强的算法都无法很好的拟合;
如果训练集的效果很好测试集很差,并且二者的差距非常大(比如10个点以上),考虑特征分布的问题,应该是有一些强特的分布在训练集和测试集上差异太大了。
如果训练集效果很好,测试集稍差一点,二者差异并不是很大,考虑调参。
GBDT为什么用CART回归树做基学习器?
基于梯度提升算法的学习器叫做GBM(Gradient Boosting Machine)。理论上,GBM可以选择各种不同的学习算法作为基学习器。现实中,用得最多的基学习器是决策树。为什么梯度提升方法倾向于选择决策树(通常是CART树)作为基学习器呢?这与决策树算法自身的优点有很大的关系。
- 决策树可以认为是if-then规则的集合,易于理解,可解释性强,预测速度快。
- 同时,决策树算法相比于其他的算法需要更少的特征工程,比如可以不用做特征标准化,可以很好的处理字段缺失的数据,也可以不用关心特征间是否相互依赖等。
- 决策树能够自动组合多个特征,它可以毫无压力地处理特征间的交互关系并且是非参数化的,因此你不必担心异常值或者数据是否线性可分(举个例子,决策树能轻松处理好类别A在某个特征维度x的末端,类别B在中间,然后类别A又出现在特征维度x前端的情况)。
- 不过,单独使用决策树算法时,有容易过拟合缺点。所幸的是,通过各种方法,抑制决策树的复杂性,降低单颗决策树的拟合能力,再通过梯度提升的方法集成多个决策树,最终能够很好的解决过拟合的问题。
由此可见,梯度提升方法和决策树学习算法可以互相取长补短,是一对完美的搭档。至于抑制单颗决策树的复杂度的方法有很多,比如限制树的最大深度、限制叶子节点的最少样本数量、限制节点分裂时的最少样本数量、吸收bagging的思想对训练样本采样(subsample),在学习单颗决策树时只使用一部分训练样本、借鉴随机森林的思路在学习单颗决策树时只采样一部分特征、在目标函数中添加正则项惩罚复杂的树结构等。
为何常规的gbdt和决策树不适用于高基数特征的场景
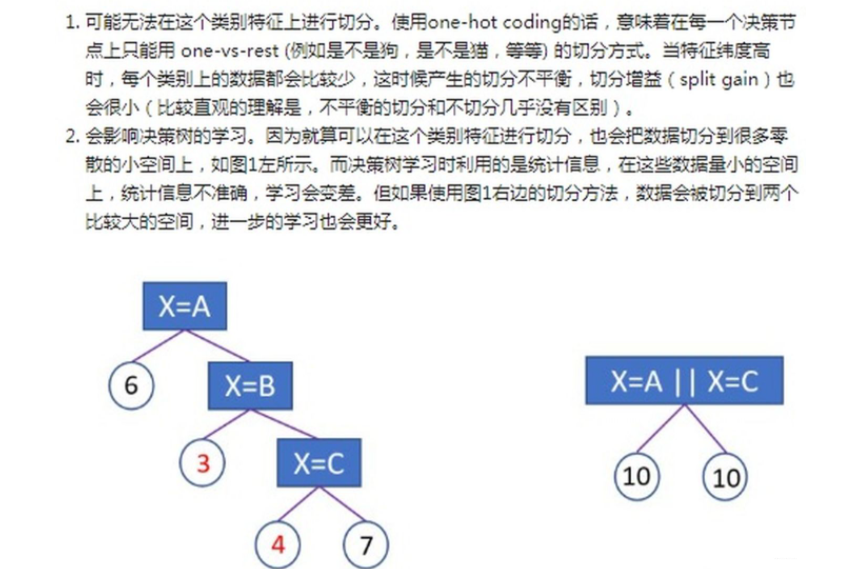
在不加限制的情况下,tree会一直在高维的稀疏特征中生长,从而像左图这样一直分裂下去,当叶子节点的样本数量很小的时候,我们难以直接就根据叶子节点的输出来判定样本的类别或者是样本的回归标签值,举一个简单的例子,加入某个叶节点一共就5个样本,4个正样本,1个负样本,那么我们可以直接判定落在这个叶子节点上的样本是正样本的概率为0.8吗?答案是不能,统计值本身就是建立在大量样本的情况下才有效,少量样本的统计特征相对于全量数据的统计特征存在严重的偏差,在样本数量很小的情况下,概率值是没有意义的。