9-正则化与标准化大总结

Pytorch官方英文文档：https://pytorch.org/docs/stable/torch.html?
Pytorch中文文档：https://pytorch-cn.readthedocs.io/zh/latest/

1. 正则化weight_decay（L2正则）

正则化从字面意思上可能一下子就懵逼，其实这是个纸老虎， 它就是一个减少方差的策略。那么这里就涉及到了一个概念方差， 什么是方差呢？

误差可分解为：偏差，方差与噪声之和。 即误差=偏差+方差+噪声

• 偏差度量了学习算法的期望预测与真实结果的偏离程度， 即刻画了学习算法本身的拟合能力
• 方差度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动所造成的影响
• 噪声则表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界。 看下面这个图：

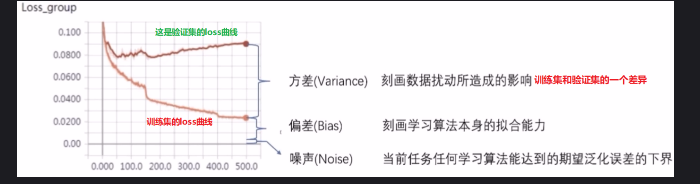
我们通常所说的过拟合现象，也就是指的高方差，就是模型在训练集上训练的超级好，几乎全部都能拟合。 但是这种情况如果换一个数据集往往就会非常差， 看看下面这个图像：

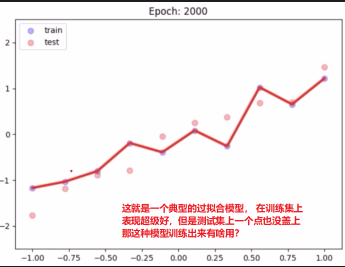
我们今天学习的正则化，其实就是再降低方差，那么就有利于解决过拟合的问题， 那么是怎么做到的呢？ 我们先来学习L1正则和L2正则。

正则化的思想就是在我们的目标函数中加个正则项， 即：

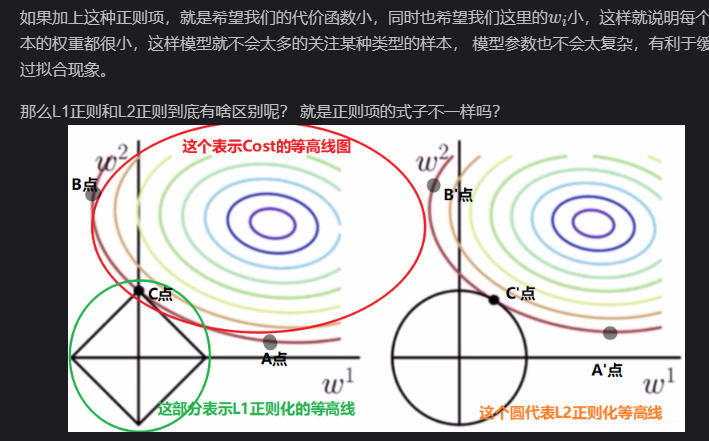
下面借这个机会也总结一下L1和L2正则化的特点（这个面试经常会问到）

L1正则化的特点：

• 不容易计算， 在零点连续但不可导， 需要分段求导
• L1模型可以将 一些权值缩小到零（稀疏）
• 执行隐式变量选择。 这意味着一些变量值对结果的影响降为0， 就像删除它们一样
• 其中一些预测因子对应较大的权值， 而其余的（几乎归零）
• 由于它可以提供稀疏的解决方案， 因此通常是建模特征数量巨大时的首选模型
• 它任意选择高度相关特征中的任何一个， 并将其余特征对应的系数减少到0
• L1范数对于异常值更具提抗力

L2正则化的特点：

• 容易计算， 可导， 适合基于梯度的方法
• 将一些权值缩小到接近0
• 相关的预测特征对应的系数值相似
• 当特征数量巨大时， 计算量会比较大
• 对于有相关特征存在的情况， 它会包含所有这些相关的特征， 但是相关特征的权值分布取决于相关性。
• 对异常值非常敏感
• 相对于L1正则会更加准确

我们下面通过代码来学习Pytorch中的L2正则项， 在Pytorch中， L2正则项又叫做weight decay(权值衰减)。那么为啥这个东西叫做权值衰减呢？ 怎么衰减了？ 我们这样看：首先，我们原来的时候， 参数的更新公式是这样的：

下面我们就通过代码来学习L2正则项：正好再来回顾一下模型训练的五个步骤

#============== step 1/5 数据 ================
def gen_data(num_data=10, x_range=(-1, 1)):
    w = 1.5
    train_x = troch.linspace(*x_range, num_data).unsqueeze_(1)
    train_y = w*train_x + torch.normal(0, 0.5, size=train_x.size())
    test_x = torch.linspace(*x_range, num_data).unsqueeze_(1)
    test_y = w*test_x + torch.normal(0, 0.3, size=test_x.size())
    
    return train_x, train_y, test_x, test_y

train_x, train_y, test_x, test_y = gen_data(x_range=(-1, 1))

#===============step 2/5 模型================
class MLP(nn.Module):
    def __init__(self, neural_num):
        super(MLP, self).__init__()
        self.linears = nn.Sequential(
            nn.Linear(1, neural_num),
            nn.ReLU(inplace=True),
            nn.Linear(neural_num, neural_num),
            nn.ReLU(inplace=True),
            nn.Linear(neural_num, neural_num),
            nn.ReLU(inplace=True),
            nn.Linear(neural_num, 1)
            )
    def forward(self, x):
        return self.linears(x)

# 这里建立两个模型，一个不带正则，一个带正则
net_normal = MLP(neural_num=200)
net_weight_decay = MLP(neural_num=200)

#===================step 3/5 优化器 ===================
optim_normal = torch.optim.SGD(net_normal.parameters(), lr=0.01, momentum=0.9)
optim_wdecay = torch.optim.SGD(net_weight_decay.parameters(), lr=0.01, momentum=0.9, weight_decay=1e-2)

#===================step 4/5  损失函数================
loss_func = torch.nn.MSELoss()

#===================step 5/5 迭代训练===================
writer = SummaryWriter(comment='_test tensorboard', filename_suffix='12345678)
for epoch in range(2000):
    # forward
    pred_normal, pred_decay = net_normal(train_x), net_weight_decay(train_x)
    loss_normal, loss_wdecay = loss_func(pred_normal, train_y), loss_func(pred_wdecay, train_y)

    optim_normal.zero_grad()
    optim_wdecay.zero_grad()

    loss_normal.backward()
    loss_wdecay.backward()

    optim_normal.step()
    optim_wdecay.step()

    if (epoch+1) % 200 == 0:
        # 可视化
        for name, layer in net_normal.named_parameters():
            writer.add_histogram(name+'_grad_normal', layer.grad, epoch)
            writer.add_histogram(name+'_data_normal', layer, epoch)

        for name, layer in net_weight_decay.named_parameters():
            writer.add_histogram(name+'_grad_weight_decay', layer.grad, epoch)
            writer.add_histogram(name+'_data_weight_decay', layer, epoch)
        
        test_pred_normal, test_pred_wdecay = net_normal(test_x), net_weight_decay(test_x)

        # 绘图
        plt.scatter(train_x.data.numpy(), train_y.data.numpy(), c='blue', s=50, alpha=0.3, label='train')
        plt.scatter(test_x.data.numpy(), test_y.data.numpy(), c='red', s=50, alpha=0.3, label='test')
        plt.plot(test_x.data.numpy(), test_pred_normal.data.numpy(), 'r-', lw=3, label='no weight decay')
        plt.plot(test_x.data.numpy(), test_pred_wdecay.data.numpy(), 'b--', lw=3, label='weight decay')
        plt.text(-0.25, -1.5, 'no weight decay loss={:.6f}'.format(loss_normal.item()), fontdict={'size': 15, 'color': 'red'})
        plt.text(-0.25, -2, 'weight decay loss={:.6f}'.format(loss_wdecay.item()), fontdict={'size': 15, 'color': 'red'})

        plt.ylim((-2.5, 2.5))
        plt.legend(loc='upper left')
        plt.title("Epoch: {}".format(epoch+1))
        plt.show()
        plt.close()

L2正则使用也比较简单，就是在优化器里面指定weight_decay这个参数即可。我们可以看一下正则化模型和不带正则化模型的效果：

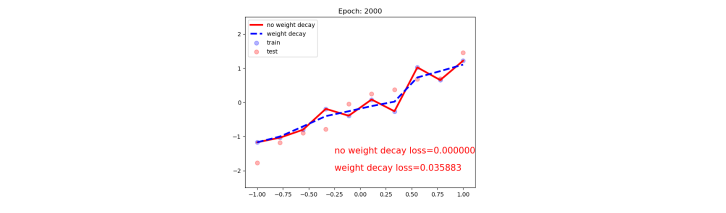
可以清楚的发现， 不带正则化的红色线发生了过拟合现象。 下面通过Tensorboard观察一下梯度参数的一个分布情况，这里面可以明显的看出衰减表示的意思：

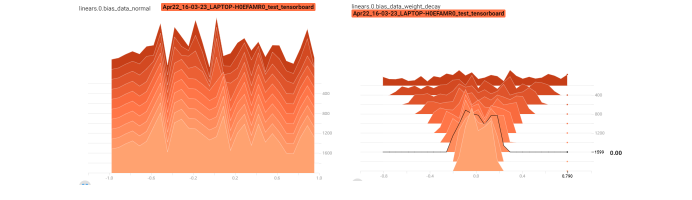
左边的是不带正则化的模型参数的分布情况，我们可以看到从迭代开始到结束整个权值的分布都没有什么变化，右边是加入了weight decay的分布， 可以看到这个衰减的趋势， 这说明L2正则起作用了，使得在迭代过程中权值在不断的缩减，以至于模型不会过于复杂产生过拟合。

那么这个L2正则是怎么实现的呢？ 我们再通过调试的方式看看背后的运行机制， 在optim_wdecay.step()这一句代码前打上断点，然后debug，步入，就进入了sgd的step方法：

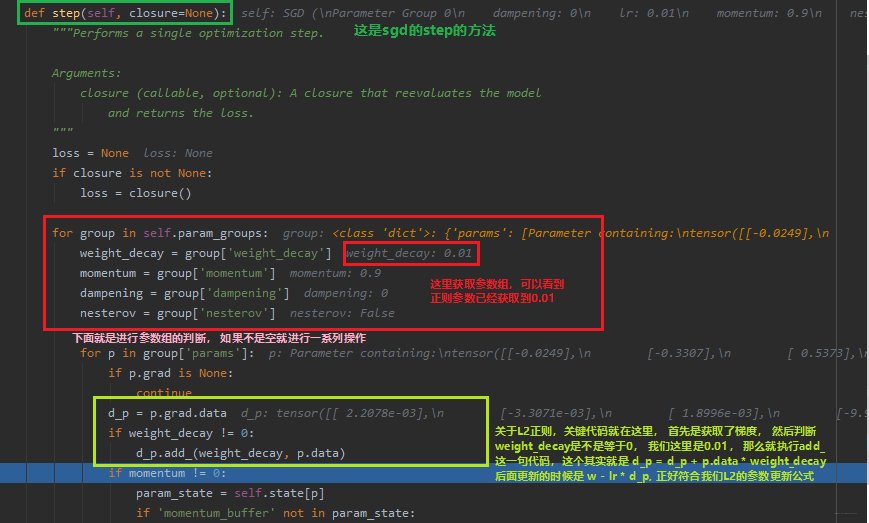
好了，L2正则化的使用和内部实现机制就到这里吧，要知道L2正则化干啥用，怎么用差不多就行了。 一般是在模型过拟合的时候用到这个方式， 当然除了L2正则化，在模型发生过拟合的时候还有其他的方式，比如Dropout，也是常用的一种方式，我们可以看看这是个什么东西？

2. 正则化之Dropout

Dropout技术也是解决过拟合问题的一个非常重要的一个手段， 那么什么叫做Dropout呢？ Dropout又应该怎么用呢？ 下面就分为两个方面来分别叙述：

2.1 Dropout概念

Dropout叫做随机失活。就是我们给出一个概率(随机)，让某个神经元的权重为0(失活)。 下面给出个图直观感受一下：

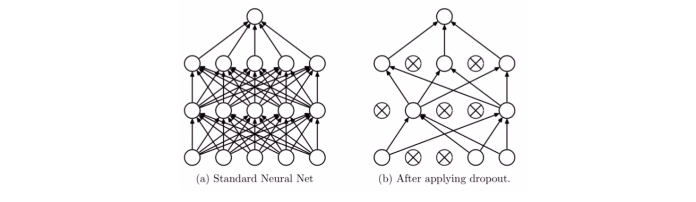
就是每一层，让某些神经元不起作用，这样就就相当于把网络进行简化了(左边和右边可以对比），我们有时候之所以会出现过拟合现象，就是因为我们的网络太复杂了，参数太多了，并且我们后面层的网络也可能太过于依赖前层的某个神经元，加入Dropout之后， 首先网络会变得简单，减少一些参数，并且由于不知道浅层的哪些神经元会失活，导致后面的网络不敢放太多的权重在前层的某个神经元，这样就减轻了一个过渡依赖的现象， 对特征少了依赖， 从而有利于缓解过拟合。 这个类似于我们期末考试的时候有没有，老师总是会给我们画出一个重点，但是由于我们不知道这些重点哪些会真的出现在试卷上，所以就得把精力分的均匀一些，都得看看， 这样保险一些，也能泛化一点，至少只要是这些类型的题都会做。 而如果我们不把精力分的均匀一些，只关注某种题型， 那么准糊一波。

好了，上面就是我们Dropout的一个原理了， 也不是太难理解，尤其是有了这个期末考试的例子， 那么关于Dropout还有一个注意的问题，就是数据的尺度变化。 这个是什么意思呢？ 我们用Dropout的时候是这样用的： 只在训练的时候开启Dropout，而测试的时候是不用Dropout的，也就是说模型训练的时候会随机失活一部分神经元， 而测试的时候我们用所有的神经元，那么这时候就会出现这个数据尺度的问题， 所以测试的时候，所有权重都乘以1-drop_prob， 以保证训练和测试时尺度变化一致， drop_prob是我们的随机失活概率。 这个应该怎么理解呢？ 我们依然拿上面那个图来说：

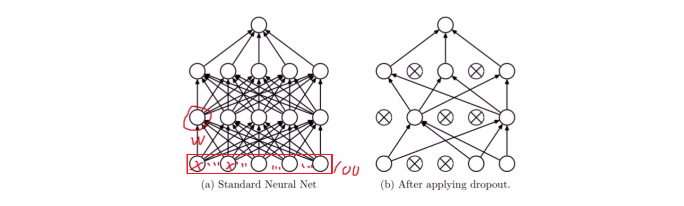
看上面这个图，假设我们的输入是100个特征， 那么第一层的第一个神经元的表达式应该是这样， 这里先假设不失活：

这样采用Dropout的训练集和不采用Dropout的测试集的尺度就变成一致了， 写代码的时候要注意这个地方。

那么，我们如何实现Dropout呢？

2.2 nn.Dropout

Pytorch中给我们提供了Dropout层， nn.Dropout

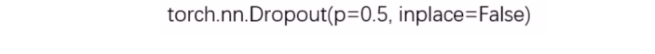
这里的p就是被舍弃概率，也就是失活概率。

下面就用上面正则化L2的代码实例看看不用L2，而是加上Dropout的效果：

# ============================ step 1/5 数据 ============================
def gen_data(num_data=10, x_range=(-1, 1)):

    w = 1.5
    train_x = torch.linspace(*x_range, num_data).unsqueeze_(1)
    train_y = w*train_x + torch.normal(0, 0.5, size=train_x.size())
    test_x = torch.linspace(*x_range, num_data).unsqueeze_(1)
    test_y = w*test_x + torch.normal(0, 0.3, size=test_x.size())

    return train_x, train_y, test_x, test_y


train_x, train_y, test_x, test_y = gen_data(x_range=(-1, 1))


# ============================ step 2/5 模型 ============================
class MLP(nn.Module):
    def __init__(self, neural_num, d_prob=0.5):
        super(MLP, self).__init__()
        self.linears = nn.Sequential(

            nn.Linear(1, neural_num),
            nn.ReLU(inplace=True),

            nn.Dropout(d_prob),             # 注意这里用上了Dropout， 我们看到这个Dropout是接在第二个Linear之前，Dropout通常放在需要Dropout网络的前一层
            nn.Linear(neural_num, neural_num),
            nn.ReLU(inplace=True),

            nn.Dropout(d_prob),
            nn.Linear(neural_num, neural_num),
            nn.ReLU(inplace=True),

            nn.Dropout(d_prob),  # 通常输出层的Dropout是不加的，这里由于数据太简单了才加上
            nn.Linear(neural_num, 1),
        )

    def forward(self, x):
        return self.linears(x)


net_prob_0 = MLP(neural_num=n_hidden, d_prob=0.)
net_prob_05 = MLP(neural_num=n_hidden, d_prob=0.5)

# ============================ step 3/5 优化器 ============================
optim_normal = torch.optim.SGD(net_prob_0.parameters(), lr=lr_init, momentum=0.9)
optim_reglar = torch.optim.SGD(net_prob_05.parameters(), lr=lr_init, momentum=0.9)

# ============================ step 4/5 损失函数 ============================
loss_func = torch.nn.MSELoss()

# ============================ step 5/5 迭代训练 ============================

writer = SummaryWriter(comment='_test_tensorboard', filename_suffix="12345678")
for epoch in range(max_iter):

    pred_normal, pred_wdecay = net_prob_0(train_x), net_prob_05(train_x)
    loss_normal, loss_wdecay = loss_func(pred_normal, train_y), loss_func(pred_wdecay, train_y)

    optim_normal.zero_grad()
    optim_reglar.zero_grad()

    loss_normal.backward()
    loss_wdecay.backward()

    optim_normal.step()
    optim_reglar.step()

    if (epoch+1) % disp_interval == 0:

        net_prob_0.eval()    # 这里要注意一下，Dropout在训练和测试阶段不一样，这时候需要对网络设置一个状态
        net_prob_05.eval() # 这个.eval()函数表示我们的网络即将使用测试状态， 设置了这个测试状态之后，才能用测试数据去测试网络， 否则网络怎么知道啥时候测试啥时候训练？

        # 可视化
        for name, layer in net_prob_0.named_parameters():
            writer.add_histogram(name + '_grad_normal', layer.grad, epoch)
            writer.add_histogram(name + '_data_normal', layer, epoch)

        for name, layer in net_prob_05.named_parameters():
            writer.add_histogram(name + '_grad_regularization', layer.grad, epoch)
            writer.add_histogram(name + '_data_regularization', layer, epoch)

        test_pred_prob_0, test_pred_prob_05 = net_prob_0(test_x), net_prob_05(test_x)

        # 绘图
        plt.scatter(train_x.data.numpy(), train_y.data.numpy(), c='blue', s=50, alpha=0.3, label='train')
        plt.scatter(test_x.data.numpy(), test_y.data.numpy(), c='red', s=50, alpha=0.3, label='test')
        plt.plot(test_x.data.numpy(), test_pred_prob_0.data.numpy(), 'r-', lw=3, label='d_prob_0')
        plt.plot(test_x.data.numpy(), test_pred_prob_05.data.numpy(), 'b--', lw=3, label='d_prob_05')
        plt.text(-0.25, -1.5, 'd_prob_0 loss={:.8f}'.format(loss_normal.item()), fontdict={'size': 15, 'color': 'red'})
        plt.text(-0.25, -2, 'd_prob_05 loss={:.6f}'.format(loss_wdecay.item()), fontdict={'size': 15, 'color': 'red'})

        plt.ylim((-2.5, 2.5))
        plt.legend(loc='upper left')
        plt.title("Epoch: {}".format(epoch+1))
        plt.show()
        plt.close()

        net_prob_0.train()   # 这里我们还得告诉网络接下来我们又要进入训练状态了
        net_prob_05.train()

所以上面的代码里面要注意两点， 第一点就是Dropout加的时候注意放置的位置，第二点就是由于Dropout操作，模型训练和测试是不一样的，上面我们说了，训练的时候采用Dropout而测试的时候不用Dropout， 那么我们在迭代的时候，就得告诉网络目前是什么状态，如果要测试，就得先用.eval()函数告诉网络一下子，训练的时候就用.train()函数告诉网络一下子。 我们下面看一下Dropout正则化后的效果：

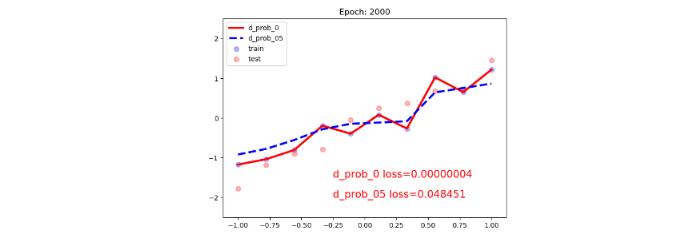
可以清楚的发现， 不带正则化的红色线发生了过拟合现象, 并且Dropout的效果和L2正则差不多，下面通过Tensorboard观察一下梯度参数的一个分布情况，看看是不是也和L2正则一样：

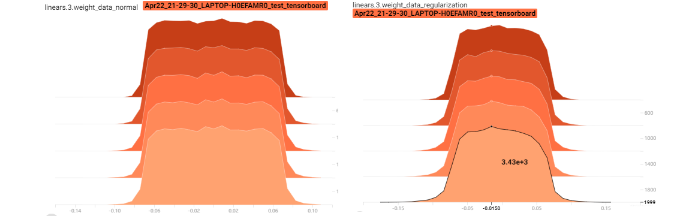
从上面这两个图，也可以看出Dropout有利于收缩权重的分布。 类似于L2的一个功能，但是这里可看不出衰减， 不信？ 我们对比一下Dropout和L2：

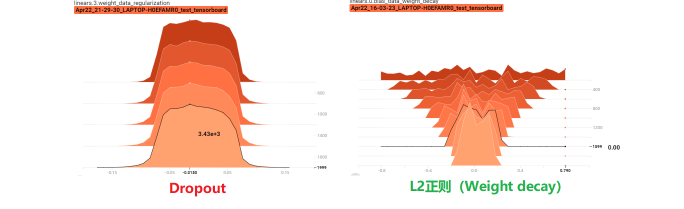
上面训练集和测试集的尺度依然是相等，并且还和原来数据的相等了。

好了，Dropout的内容就是这些了，下面我们还要学习一个在网络中很实用的一个技术叫做BatchNormalization。

3. 标准化之BatchNormalization

3.1 BatchNormalization是什么以及为啥用？

BatchNormalization就是批标准化， 批指的是mini-batch, 标准化也就是0均值1方差，看似这个东西比较简单，但是威力却是很强， 有下面几个优点（来自2015年原文《BatchNormalization：Accelerating Deep Network Train by Reducing Internal Covariate Shift》， 这篇论文堪称这一年深度学习界最重要的一篇论文）：

• 可以用更大学习率，加速模型收敛
• 可以不用精心设计权值初始化
• 可以不用Dropout或者较小的Dropout
• 可以不用L2或者较小的weight decay
• 可以不用局部响应标准化（AlexNet中用到过

好了，既然优点辣么多，肯定是要好好学习这个方法， 那么下面就看看到底BatchNormlization是怎么做到这么强大的， 计算方式到底是啥？下面就是BatchNormlization的算法流程：

BatchNormlization（BN）既然这么简单，为啥能起那么大的作用呢？ 其实这里BN有点无心插柳柳成荫的感觉，可以看一下上面BN论文的标题，会发现这个算法提出本来是想解决Internal Covariate Shift这个问题的，这个问题在权重初始化那里介绍过，就是网络输出层的数值尺度的变化导致网络无法训练：

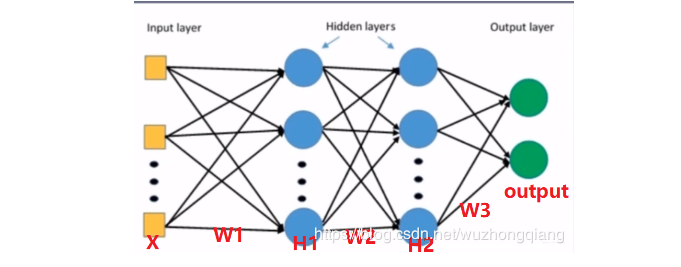
还记得这几个公式吗：

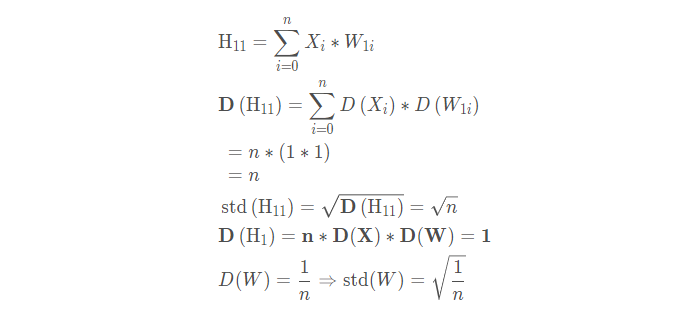
我们发现每一层的方差竟然是前面所有层方差的连乘，那么假设有一层尺度上有点不正常，那么随着网络的加深，很容易引起梯度消失或者爆炸。所以权值初始化那里就考虑采用一种初始化的方式控制网络输出层的一个尺度。 所以BN的提出， 也是为了解决这个问题的，只不过解决了这个问题之后，竟然发现带来了一系列的优点，上面提到的那些。

下面就通过代码看一下，加了BN之后，为啥不用精心的设置权值初始化了， 依然是权值初始化那里的那份代码：

class MLP(nn.Module):
    def __init__(self, neural_num, layers=100):
        super(MLP, self).__init__()
        self.linears = nn.ModuleList([nn.Linear(neural_num, neural_num, bias=False) for i in range(layers)])
        self.bns = nn.ModuleList([nn.BatchNorm1d(neural_num) for i in range(layers)])
        self.neural_num = neural_num

    def forward(self, x):

        for (i, linear), bn in zip(enumerate(self.linears), self.bns):
            x = linear(x)
            # x = bn(x)
            x = torch.relu(x)

            if torch.isnan(x.std()):
                print("output is nan in {} layers".format(i))
                break

            print("layers:{}, std:{}".format(i, x.std().item()))

        return x

    def initialize(self):
        for m in self.modules():
            if isinstance(m, nn.Linear):

                # method 1
                # nn.init.normal_(m.weight.data, std=1)    # normal: mean=0, std=1

                # method 2 kaiming
                nn.init.kaiming_normal_(m.weight.data)


neural_nums = 256
layer_nums = 100
batch_size = 16

net = MLP(neural_nums, layer_nums)
# net.initialize()

inputs = torch.randn((batch_size, neural_nums))  # normal: mean=0, std=1

output = net(inputs)
print(output)

首先我们先不用权值初始化，不用BN， 看看网络出现的问题：

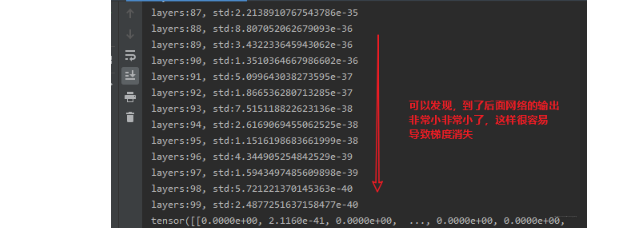
那么我们加上权值初始化，由于网络里面用到了relu， 所以这里使用Kaiming初始化方法， 看下效果：

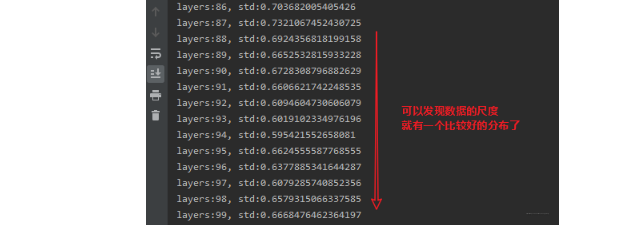
这里是我们精心设计了权值初始化的一个方法，考虑到relu,我们得用Kaiming初始化，考虑到tanh，我们还得用Xavier， 还是挺复杂的， 那么我们假设不用权值初始化，而是在网络层的激活函数前加上BN呢？

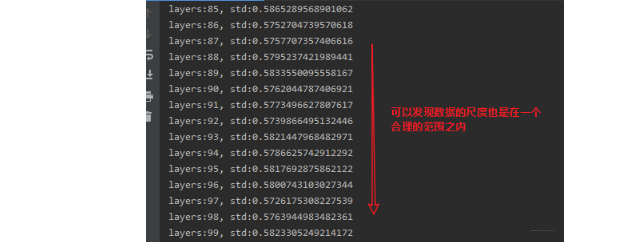
可以发现，强大的BN依然可以保证数据的尺度，并且好处就是我们不用再考虑用什么样的方式进行权值的初始化。下面再从人民币二分类的实验中就加权值初始化，加BN和啥都不加三者产生的一个效果：

这里也可以看出BN层的作用，可以约束我们特征输入层的一个尺度范围，让它保持一个良好的分布，让模型训练起来更加简单。

3.2 Pytorch中的BatchNormalization

Pytorch中提供了三种BatchNorm方法：

• nn.BatchNorm1d
• nn.BatchNorm2d
• nn.BatchNorm3d

上面三个BatchNorm方法都继承__BatchNorm这个基类，初始化参数如下：

这里的num_features表示一个样本的特征数量，这是最重要的一个参数。eps表示分母修正项， momentum表示指数加权平均估计当前mean/var。 affine表示是否需要affine transform, track_running_stats表示是训练状态还是测试状态，这个也是非常关键的，因为我们发现momentum那里有个均值和方差，如果是训练状态，那么就需要重新估计mean和方差，而如果是测试状态，就用训练时候统计的均值和方差。

而BatchNorm的三个方法也是有属性的：

running_mean: 均值
running_var: 方差
weight: affine transform中的γ
bias: affine transforom中的β

这四个属性分别对应我们公式中用到的四个属性：

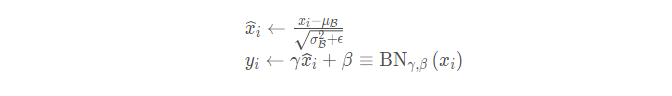
这里的均值和方差是采用指数加权平均进行计算的， 不仅要考虑当前mini-batch的均值和方差，还考虑上一个mini-batch的均值和方差（当然是在训练的时候，测试的时候是用当前的统计值。）

running_mean = (1-momentum) * pre_running_mean + momentum * mean_t
running_var = (1-momentum) * pre_running_var + momentum * var_t

了解了三个方法的基本属性，下面得看看这三个方法到底用的时候有啥区别？

• nn.BatchNorm1d -> input = B * 特征数 * 1d特征

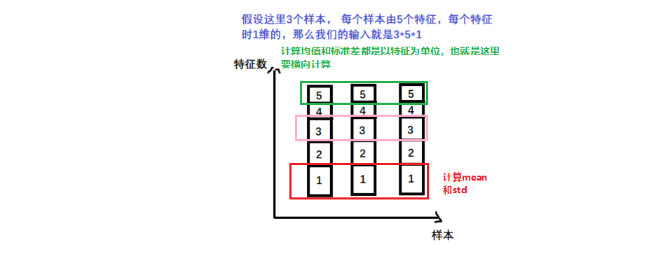
下面直接动过代码看看上面这个一维的这个BN方法要怎么用：

batch_size = 3    # 3个样本
num_features = 5    # 5个特征
momentum = 0.3     # 这个计算后面均值，方差的时候用到

features_shape = (1)   # 我们特征的维度是1

feature_map = torch.ones(features_shape)                                                    # 1D   一个特征
feature_maps = torch.stack([feature_map*(i+1) for i in range(num_features)], dim=0)         # 2D   一列数据
feature_maps_bs = torch.stack([feature_maps for i in range(batch_size)], dim=0)             # 3D   上面那3列数据
print("input data:\n{} shape is {}".format(feature_maps_bs, feature_maps_bs.shape))

bn = nn.BatchNorm1d(num_features=num_features, momentum=momentum)   # BN1d在这里定义

running_mean, running_var = 0, 1   # 这个得初始化，毕竟我们这是第一次迭代

for i in range(2):
    outputs = bn(feature_maps_bs)

    print("\niteration:{}, running mean: {} ".format(i, bn.running_mean))
    print("iteration:{}, running var:{} ".format(i, bn.running_var))

    mean_t, var_t = 2, 0

    running_mean = (1 - momentum) * running_mean + momentum * mean_t         # 采用滑动平均方式计算均值和方差
    running_var = (1 - momentum) * running_var + momentum * var_t

    print("iteration:{}, 第二个特征的running mean: {} ".format(i, running_mean))
    print("iteration:{}, 第二个特征的running var:{}".format(i, running_var))

下面看一下结果：

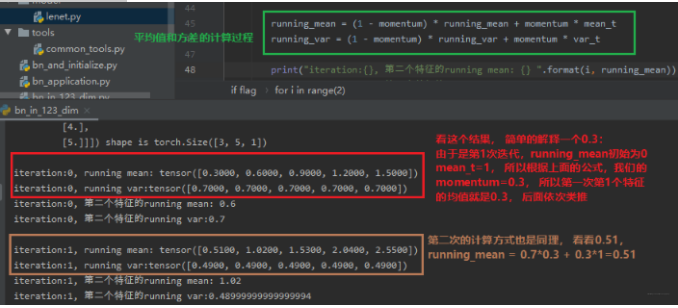
所以我们得知道，当前mini-bath所得到的用于对数据进行Normalize的这个均值，不是当前mini-batch得到的均值，而是会考虑前面mini-batch的数据信息， 加权平均的一个均值和方差。下面通过调试看看BN里面的四个非常重要的参数：均值，方差， gamma和beta它们的shape：

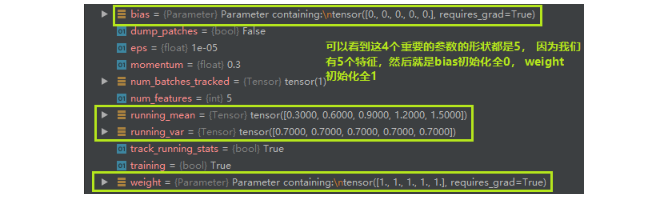
• nn.BatchNorm2d -> input = B * 特征数 * 2d特征

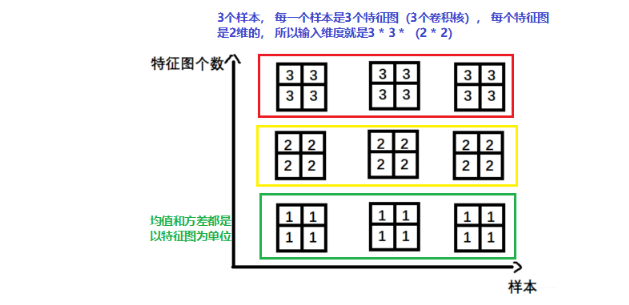
卷积图像中经常是这种2d的。

• nn.BatchNorm3d -> input = B * 特征数 * 3d特征

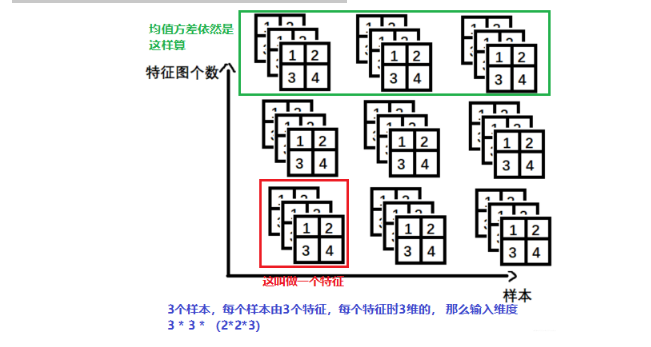
这个在时空序列中会用到。

这就是BatchNormalization的内容了，下面再学习一些其他的Normalization的一些知识。

3.3 其他的Normalization方法

我们常见的Normalization方法其实有四种，分别是Batch Normalization(BN)、Layer Normalization(LN)、Instance Normalization(IN)、Group Normalization(GN)。这四种方式既然都是Normalization，那么有什么相同点和异同点呢？

相同点就是公式上：

1.Layer Normalization

起因： BN不适用于变长的网络，如RNN， 所以提出了逐层计算均值和方差的思路。

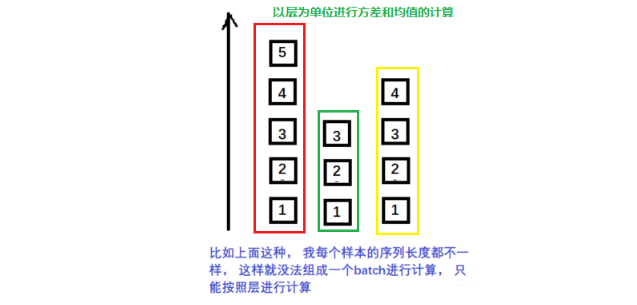
BN与LN的区别：

• LN中同层神经元输入拥有相同的均值和方差，不同的输入样本有不同的均值和方差；
• BN中则针对不同神经元输入计算均值和方差，同一个batch中的输入拥有相同的均值和方差。

还要注意， 在LN中不再有running_mean和running_var， 并且gamma和beta为逐元素的。 下面我们看看Pytorch中的LN：

nn.LayerNorm(normalized_shape, eps=1e-05, elementwise_affine=True)

这里的normalized_shape表示该层特征形状，这个依然是最重要的。 eps表示分母修正项， elementwise_affine表示是否需要affine transform。

好了， 下面又得看看怎么用了，它是怎么进行计算的， 这个才是关键， LayerNorm 常用在RNN当中，在CNN和FCN中不如BN的效果好。

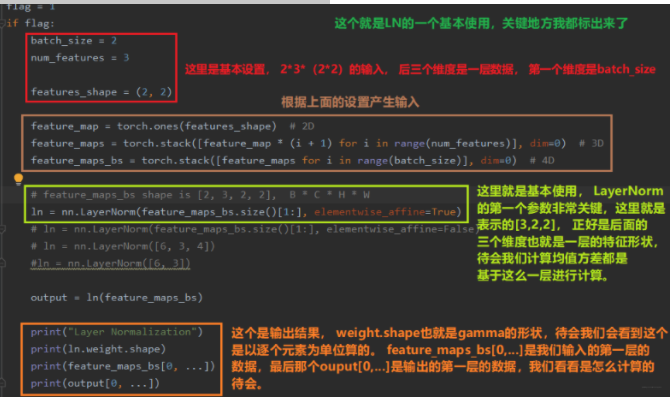
上面是代码部分， 下面我们看看结果：

所以从这里我们也能基本上看出LN和BN的一个区别了， LN它是以层为单位的， 而BN是以batch为单位的，后面还有个神图， 一看就差不多知道这几种标准化方法到底是怎么算的了。

如果我们把参数elementwise_affine设置为False， 会报AttributeError: 'NoneType' object has no attribute 'shape'， 另外还得说一下normalized_shape， 这个我们也可以自己指定， 但得注意一定要从最后维度开始， 这是啥意思？

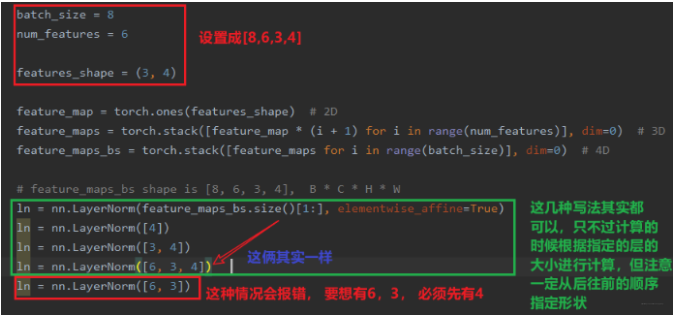
最后这种情况的报错：

RuntimeError: Given normalized_shape=[6, 3], expected input with shape [*, 6, 3], but got input of size[8, 6, 3, 4]

2.Instance Normalization

起因： BN在图像生成中不适用， 思路就是逐个Instance(channel)计算均值和方差。比如在图像风格迁移中，每一个样本的风格是不一样的，所以我们不能像BN那样从多个样本里面去计算平均值和方差了。那么应该怎么算呢？ 还是以上面的一个图为例：

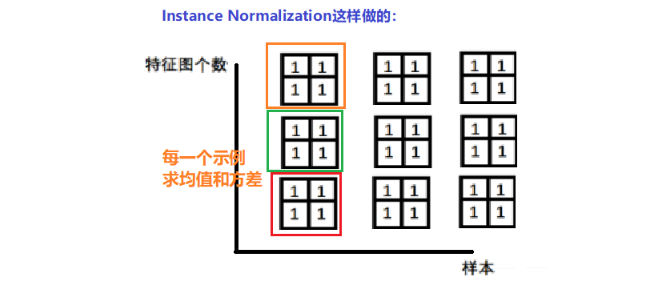
下面看看Pytorch提供的InstanceNorm这个网络层怎么使用：

nn.InstanceNorm2d(num_features, eps=1e-05, momentum=0.1, affine=False, track_running_stats=False)

这里的num_features表示一个样本的特征数量(最重要), eps表示分母修正项， momentum指数加权平均估计当前的mean/var， affine是否需要affine transform, track_running_stats表示训练状态还是测试状态。这个和BN的参数是一样的，并且也有1d/2d/3d， 当然区分方法和BN那边一样。 下面依然是代码中看一下Instance Normalization是如何计算的：

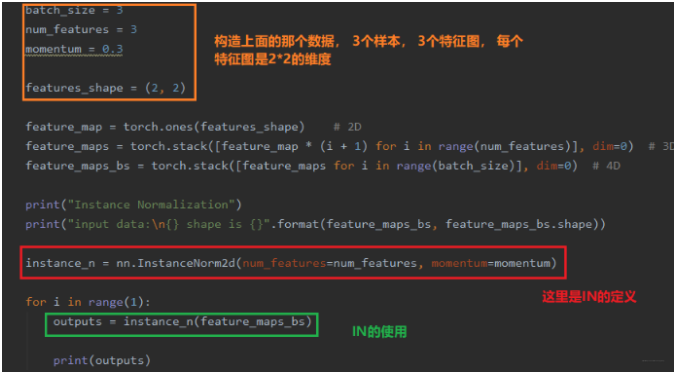
下面看看结果：

3.Group Normalization

起因： 小batch样本中， BN估计的值不准， 这种Normalization的思路就是数据不够， 通道来凑。 一样用于大模型（小batch size）的任务。

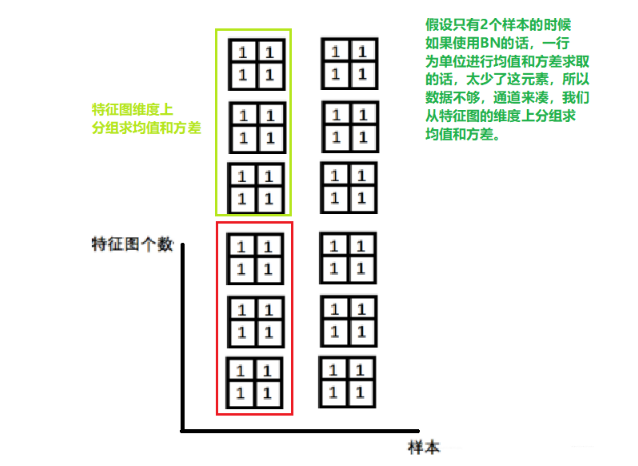
这个有点LayerNorm的感觉，只不过相当于LayerNorm进行了分组， 这个和LN一样，不再有running_mean和running_var， gamma和beta为逐个通道的。看看Pytorch提供的GroupNorm：

nn.GroupNorm(num_groups, num_channels, eps=1e-05, affine=True)

num_groups表示分组数， num_channels表示通道数（特征数）， eps表示分母修正项， affine是否需要affine transform。 这里前两个参数是必须的，要不然机器也不知道你要咋分组，每组多少个等。 提供了组数和通道数，两者的商就代表一组是多少个特征图， 这样从一组中求平均和方差。还要注意分组的时候要能整除。下面也是从代码中看看怎么用：

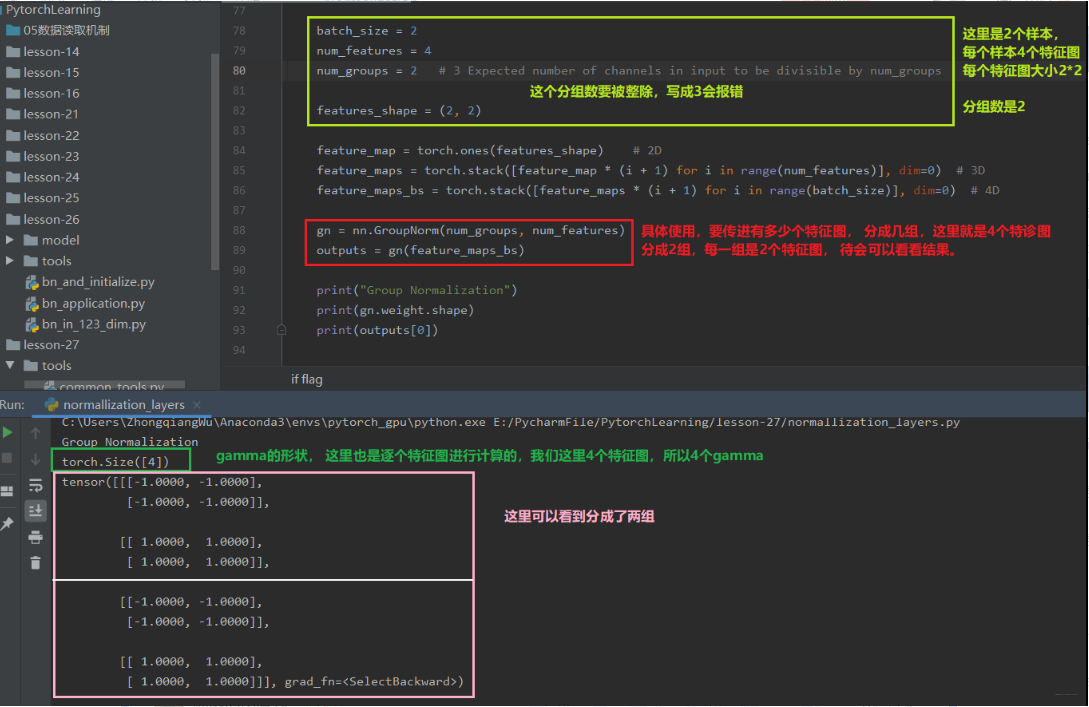
好了，上面就是四种标准化方法了， BN， LN， IN和GN都是为了克服Internal Covariate Shift(ICS)提出来的，它们的计算公式差不多，只不过计算均值和方差的时候采用的方式不同， 下面来一个神图：

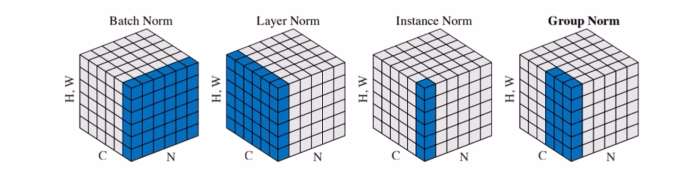
好吧，这个图把四维的数据画成了维的，如果不太好理解的话， 那么就采用上面的几个图理解一下， 把上面四种方式的计算合起来：

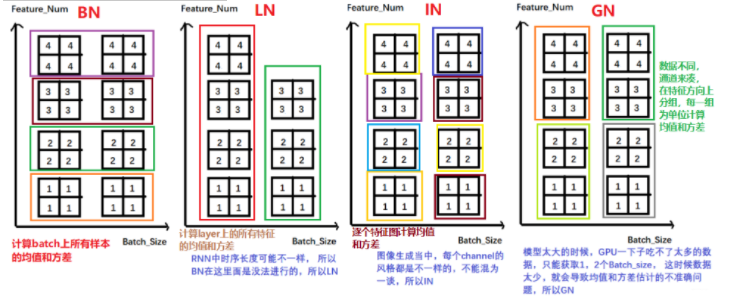
关于这四种方法的详细介绍，可以参考这篇文章https://blog.csdn.net/liuxiao214/article/details/81037416

4. 总结

这次的学习内容就到这里了，这次的整理依然挺多， 主要是总结了一下Pytorch中常用的正则化和标准化的一些方法，依然是快速梳理一遍。

首先是正则化那块，正则化主要是缓解模型的过拟合问题，我们从L2正则化开始，L2正则化也叫权重衰减，我们学习了L2正则的原理，L1正则和L2正则的区别，然后学习了L2正则在Pytorch中的使用。 然后又学习了Dropout正则化，依然是原理和使用，并且对比了一下L2正则和Dropout正则的效果。

标准化主要是解决网络层输出的数据尺度变化不一致的问题， 首先学习了Batch Normalization，这个非常重要，有很多的优点， 学习了它的原理和具体的使用方法，然后又介绍了其他三种标准化方法， LayerNorm Normalization、Instance Normalization和Group Normalization， 分别看了一下是如何计算的并且在Pytorch中如何使用的。 最后对比了一下这四种方法。

下面依然是一张思维导图把知识拎起来：

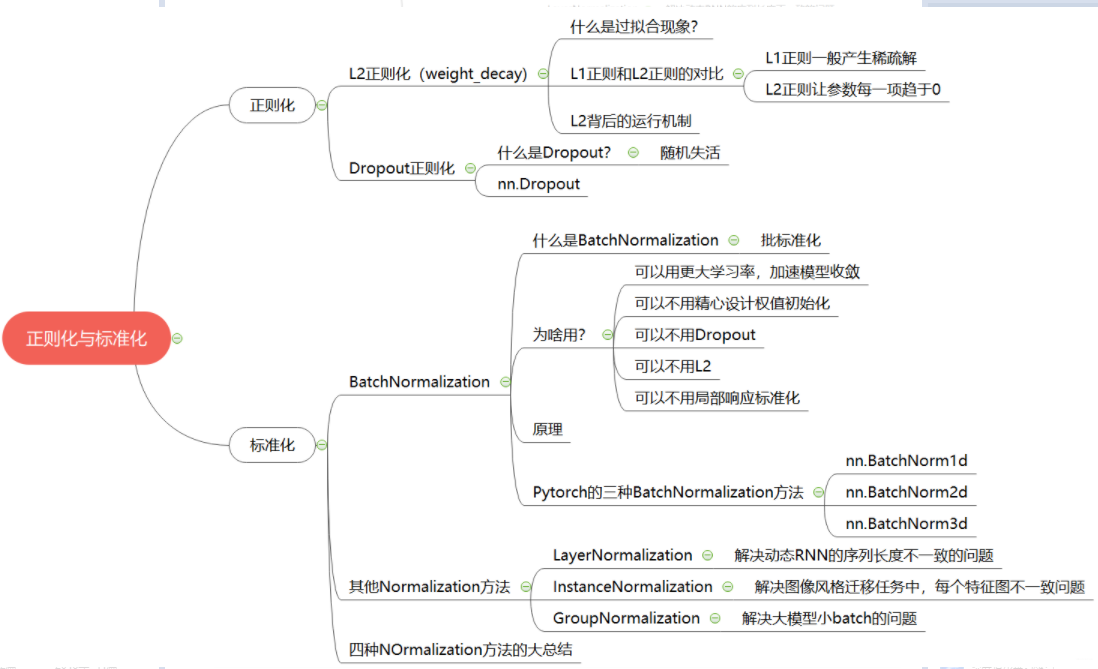
好了， 到这里为止，关于机器学习模型训练的五个步骤的细节部分就结束了， 我们从数据模块捋一捋， 数据模块，主要学习了DataLoader和Dataset的工作原理，构建数据生成器， 还顺带着学习了transforms处理图像。模型模块，学习了Module， 模型容器， 还有各种卷积，池化，激活函数等层， 还学习了数据初始化的一些方法。 损失函数模块，介绍了各种损失函数的使用。 优化器模块，介绍了优化器和学习率调整策略。 迭代训练模块学习了Tensorboard可视化方法，学习了正则化和标准化。 通过上面的学习，基本上可以把机器学习模型训练的五个步骤的各个细节搭建一个框架出来了。

最后打算再安排一篇类似后记的东西，通过上面五个步骤，我们就可以通过Pytorch搭建一个模型并且进行有效的训练，而模型搭建完了之后我们要保存下来，以备后面的使用，并且在大型任务中我们不可能从头自己搭建模型，往往需要模型的迁移， 为了提高训练效率，我们往往需要使用GPU， 最后再整理一些Pytorch中常见的报错作为结束。 所以下一篇的内容，我们从模型的保存与加载， 模型的微调技术， GPU使用和Pytorch常见报错四方面来整理。 最后一篇了，继续Rush吧 😉