1. 写在前面
最近在补ML和DL的相关基础,发现有些非常重要的知识还是了解的太表面,甚至可以说不知其然也不知其所以然了,所以这段时间想借着找工作的这个机会,通过学习一些优秀的文章,来慢慢的把这块短板也补上来。今天学习的这篇文章是交叉熵损失和平方损失,虽然我们一看这俩东西,可能瞬间感觉非常简单吗不是,公式甚至都能不假思索的就写出来,这还有啥不知其然和所以然的,哈哈,好吧,反正我是觉得我没理太明白,所以想重新记录学习下。
拿一个最基本的面试题来说: 为啥二分类问题里面会用到交叉熵损失,而不用平方损失呢? 既然sigmoid输出的是概率值,难道用这个概率值与真实的label0或者1求平方损失,然后更新参数不可以吗?
如果感觉也能不假思索的张口就来,那么应该是真掌握了,可以回退了哈哈,如果感觉还不大行,那么就可以往下看看;)。
这篇文章是转载的一篇文章, 原文来自https://blog.csdn.net/weixin_41888257/article/details/104894141,想了解更多,可以去看原文章。
因为我比较喜欢发现比较好的文章,就转载下,但是转载的同时,会添加自己的一些理解, 这样感觉会比简单的看一遍会有效果。下面开始正文。
2. 概念区别
首先先理清楚这两个损失的概念:

3. 为什么不用MSE(两者的区别详解)
3.1 原因1:交叉熵loss权重更新更快
3.1.1 MSE
先看看MSE, 比如对于一个神经元(单输入单输出,sigmoid函数),定义其代价函数为:

sigmoid的函数图像我们都知道:
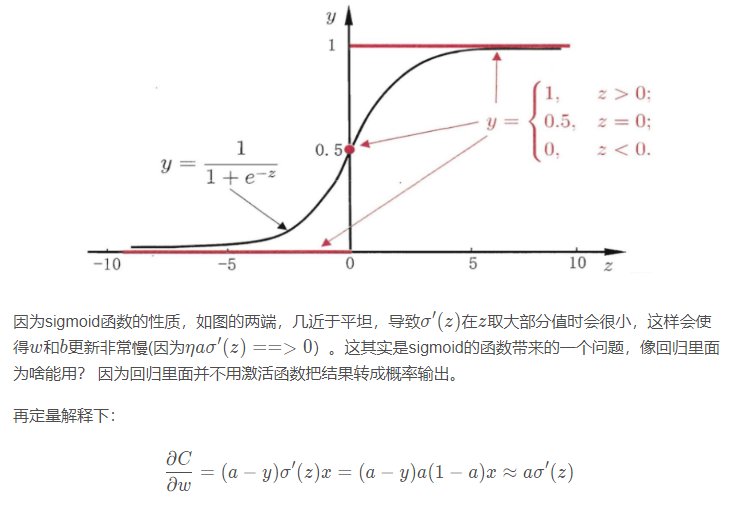

也就是平方损失(MSE)的梯度更新很慢
还有个问题,就是会发现不管真实值是多少,只要输出值预测的是0或者1,那么梯度都是0. 这其实说明当采用MSE的时候,梯度很小的时候,根本就看不出来是离真实目标很远还是很近。 这就带来实际操作的问题当梯度很小的时候,应该减小步长(否则容易在最优解附近来回震荡), 而用MSE的时候,显然这个操作是不太好进行的,梯度很小的时候,有可能是离真实值还超级远呢。
3.1.2 交叉熵损失
为了克服上述 MSE 不足,引入了categorical_crossentropy(交叉熵损失函数), 二分类交叉熵损失函数

推导过程依然是需要张口就来。这个求导过程不是很难,可以用链式法则一点点的走,来试试看:


可以看作是Sigmoid的一般情况,用于多分类问题。
损失函数:
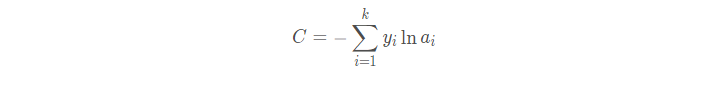
这个东西涉及到softmax求导了,具体看这里吧, 但后续的分析和上面类似。
那么交叉熵损失的缺点是啥呢?
sigmoid(softmax)+cross-entropy loss 擅长于学习类间的信息,因为它采用了类间竞争机制,它只关心对于正确标签预测概率的准确性,忽略了其他非正确标签的差异,导致学习到的特征比较散。基于这个问题的优化有很多,比如对softmax进行改进,如L-Softmax、SM-Softmax、AM-Softmax等。这些在本篇不展开讨论。
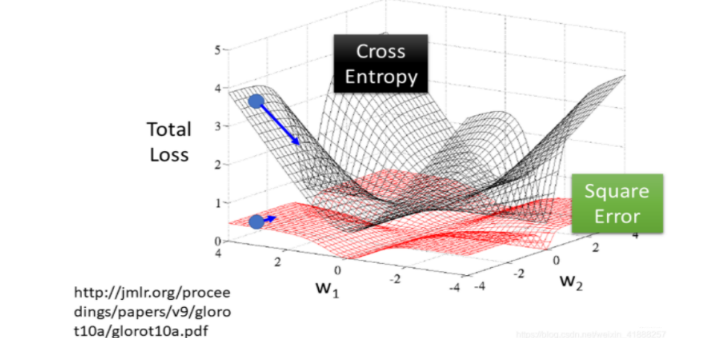
3.2 原因2: MSE是非凸优化问题而Cross-entropy是凸优化问题
3.2.1 MSE
我们从最简单的线性回归开始讨论:
线性回归(回归问题)使用的是平方损失:
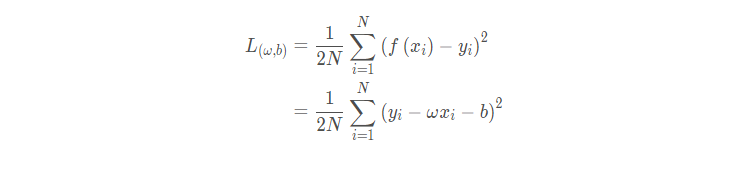

上式是非凸的,不能直接求解析解,而且不宜优化,易陷入局部最优解,即使使用梯度下降也很难得到全局最优解。如下图所示:
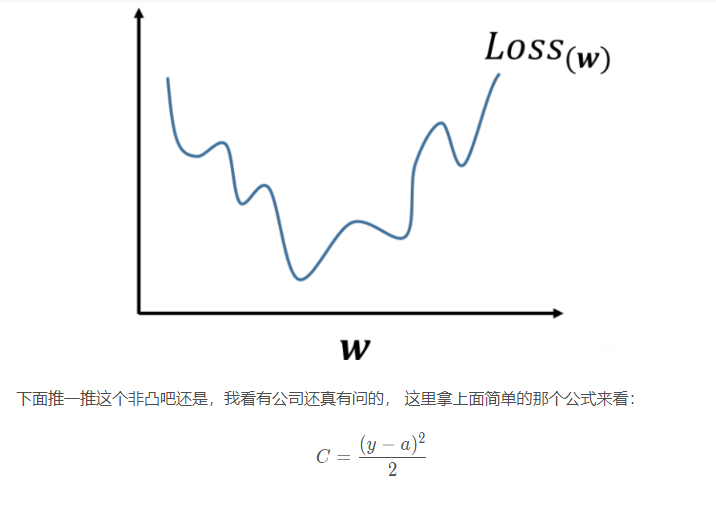

3.2.2 Cross-entropy
Cross-entropy 计算 loss,则依旧是一个凸优化问题。下面进行推导:

对数似然函数:

这样一来,问题就变成了以对数似然函数为目标函数的最优化问题,逻辑回归中通常的方法就是梯度下降法和拟牛顿法。
极大似然函数是求极大,取个相反数,再对所有N NN个样本取平均,即得到逻辑回归的损失函数:

其中:
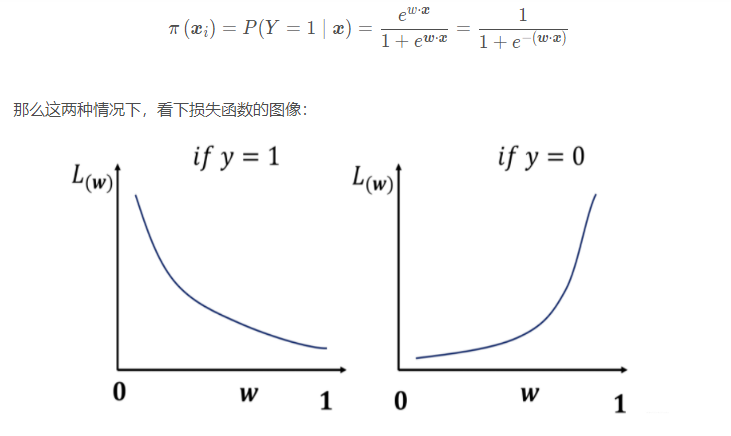
当类别标签为y = 1 y=1y=1的时候,越靠近1则损失越小;当类别标签y = 0 y=0y=0的时候,越靠近1,损失就越大。
4. 总结
分类问题,都用 one-hot + Cross-entropy。之所以在分类问题中不用MSE,主要是上面的两个原因① 参数更新缓慢 ②非凸优化问题
training 过程中,分类问题用 Cross-entropy,回归问题用 mean squared error。

这个问题终于理清楚了,你明白啦吗? 如果不明白,可以参考原博客链接再去理解理解。