1. 写在前面
最近做一个时空序列预测的一个问题,用到了数据归一化和标准化,之前一直想花点时间看一下这俩的区别究竟是啥? 现在参考了几篇博文,加上自己的一些理解,来具体的总结总结。
数据的归一化是无量纲化,也就是忽略掉特征之间值大小对最后结果带来的影响,而标准化是统一特征的数据分布,忽略掉不同分布的特征对最后结果带来的影响
首先给出sklearn中归一化和标准化的实现方法:
1 | from sklearn.preprocessing import MinMaxScaler, StandardScaler |
有时候归一化也叫做normalization,千万不要让这个英语导致和标准化混了。
2. 概念剖析
2.1 归一化
把数据变成0-1或者-1-1之间的小数。主要是为了数据处理方便提出来的,把数据映射到0~1范围之内处理,更加便捷快速
把有量纲表达式变成无量纲表达式,便于不同单位或量级的指标能够进行比较和加权。归一化是一种简化计算的方式,即将有量纲的表达式,经过变换,化为无量纲的表达式,成为纯量。
1 |
|
2.2 标准化
在机器学习中,我们可能要处理不同种类的资料,例如,音讯和图片上的像素值,这些资料可能是高维度的,资料标准化后会使每个特征中的数值平均变为0(将每个特征的值都减掉原始资料中该特征的平均)、标准差变为1,这个方法被广泛的使用在许多机器学习算法中(例如:支持向量机、逻辑回归和类神经网络)。
1 | (1)Z-score规范化(标准差标准化 / 零均值标准化) |
中心化:平均值为0,对标准差无要求
1 | x' = x - μ |
归一化和标准化的区别:归一化是将样本的特征值转换到同一量纲下把数据映射到[0,1]或者[-1, 1]区间内,仅由变量的极值决定,因区间放缩法是归一化的一种。标准化是依照特征矩阵的列处理数据,其通过求z-score的方法,转换为标准正态分布,和整体样本分布相关,每个样本点都能对标准化产生影响。它们的相同点在于都能取消由于量纲不同引起的误差;都是一种线性变换,都是对向量X按照比例压缩再进行平移。
标准化和中心化的区别:标准化是原始分数减去平均数然后除以标准差,中心化是原始分数减去平均数。 所以一般流程为先中心化再标准化。
无量纲:我的理解就是通过某种方法能去掉实际过程中的单位,从而简化计算。
3. 理解
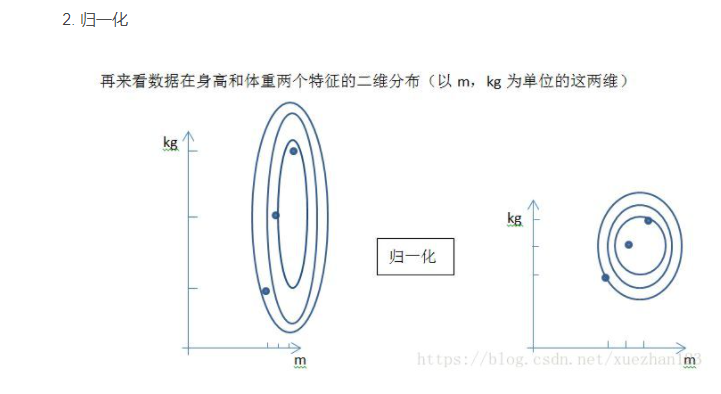
归一化特点:
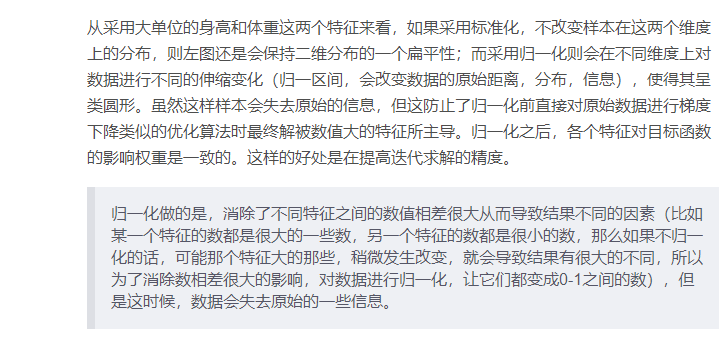
对不同特征维度的伸缩变换的目的是使各个特征维度对目标函数的影响权重是一致的,即使得那些扁平分布的数据伸缩变换成类圆形。这也就改变了原始数据的一个分布。
好处:- 提高迭代求解的收敛速度
- 提高迭代求解的精度
标准化特点:
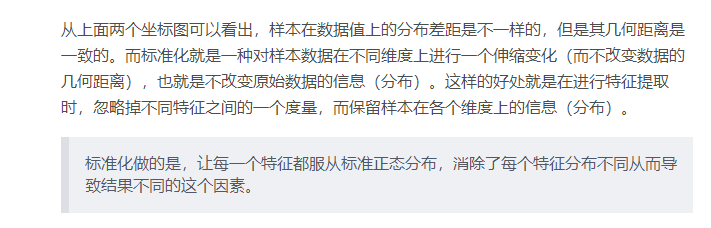
对不同特征维度的伸缩变换的目的是使得不同度量之间的特征具有可比性。同时不改变原始数据的分布。
好处:- 使得不同度量之间的特征具有可比性,对目标函数的影响体现在几何分布上,而不是数值上
- 不改变原始数据的分布
举个例子看一下:
根据人的身高和体重预测人的健康指数
假设有如下原始样本数据是四维的
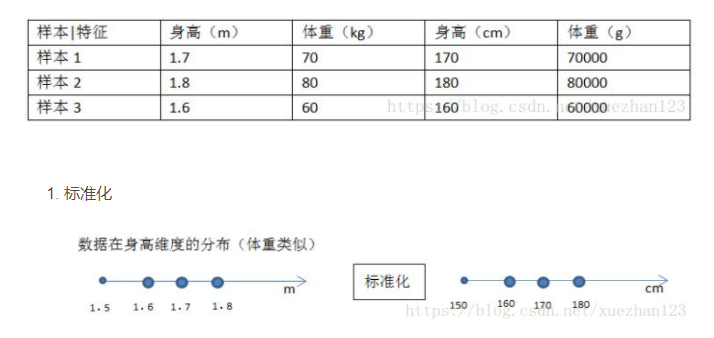
但是要明确: 归一化和标准化的相同点都是对某个特征进行缩放而不是对某个样本的特征向量进行缩放。 对特征向量缩放是毫无意义的。 比如三列特征:身高、体重、血压。每一条样本(row)就是三个这样的值,对这个row无论是进行标准化还是归一化都是好笑的,因为你不能将身高、体重和血压混到一起去!
在线性代数中,将一个向量除以向量的长度,也被称为标准化,不过这里的标准化是将向量变为长度为1的单位向量,它和我们这里的标准化不是一回事儿,不能搞混(暗坑2)。
4. 为什么需要归一化/标准化
如前文所说,归一化/标准化实质是一种线性变换,线性变换有很多良好的性质,这些性质决定了对数据改变后不会造成“失效”,反而能提高数据的表现,这些性质是归一化/标准化的前提。比如有一个很重要的性质:线性变换不会改变原始数据的数值排序。
某些模型求解需要
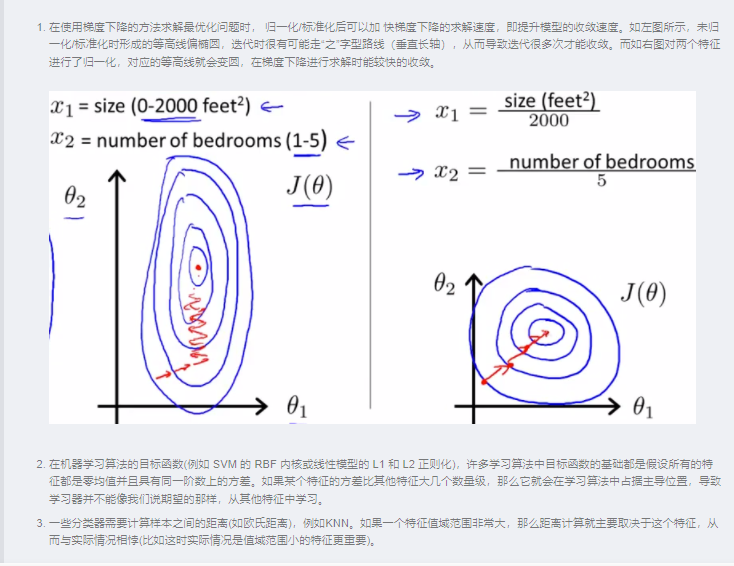
经验上说,归一化是让不同维度之间的特征在数值上有一定比较性,可以大大提高分类器的准确性。
无量纲化
例如房子数量和收入,因为从业务层知道,这两者的重要性一样,所以把它们全部归一化。 这是从业务层面上作的处理。避免数值问题
太大的数会引发数值问题。
5. 使用场景
首先明确,在机器学习中,标准化是更常用的手段,归一化的应用场景是有限的。原因有两点:
标准化更好保持了样本间距
当样本中有异常点时,归一化有可能将正常的样本“挤”到一起去。比如三个样本,某个特征的值为1,2,10000,假设10000这个值是异常值,用归一化的方法后,正常的1,2就会被“挤”到一起去。如果不幸的是1和2的分类标签还是相反的,那么,当我们用梯度下降来做分类模型训练时,模型会需要更长的时间收敛,因为将样本分开需要更大的努力!而标准化在这方面就做得很好,至少它不会将样本“挤到一起”。
标准化更符合统计学假设
对一个数值特征来说,很大可能它是服从正态分布的。标准化其实是基于这个隐含假设,只不过是略施小技,将这个正态分布调整为均值为0,方差为1的标准正态分布而已。
下面看下具体的使用场景:
- 如果对输出结果范围有要求,用归一化。
- 如果数据较为稳定,不存在极端的最大最小值,用归一化。
- 如果数据存在异常值和较多噪音,用标准化,可以间接通过中心化避免
异常值和极端值的影响。

6. 逻辑回归必须要进行标准化吗?
面试的时候,无论回答必须或者不必须,都是错的!!!
6.1 是否正则化
真正的答案是,这取决于我们的逻辑回归是不是用正则。
- 如果不用正则, 那么标准化不是必须的
- 如果用正则,那么标准化是必须的
为什么呢?
因为不用正则时,我们的损失函数只是仅仅在度量预测与真实的差距,加上正则后,我们的损失函数除了要度量上面的差距外,还要度量参数值是否足够小。而参数值的大小程度或者说大小的级别是与特征的数值范围相关的。
举例来说,我们用体重预测身高,体重用kg衡量时,训练出的模型是:
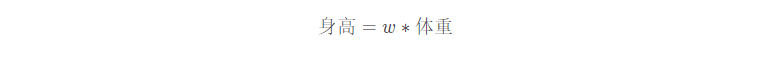
w就是我们训练出来的参数。
在我们的体重用吨来衡量时,w ww的值就会扩大为原来的1000倍。在上面两种情况,都用L1正则的话,显然对模型的训练影响不同。
假如不同的特征数值范围不一样,有的是0到0.1,有的是100到10000,那么,每个特征对应的参数大小级别也会不一样,在 L1 正则时,我们是简单将参数的绝对值相加,因为它们的大小级别不一样,就会导致 L1 最后只会对那些级别比较大的参数有作用,那些小的参数都被忽略了。
6.2 标准化对LR的好处
如果你回答到这里,面试官应该基本满意了,但是他可能会进一步考察你,如果不用正则,那么标准化对逻辑回归有什么好处吗?
答案是有好处,进行标准化后,我们得出的参数值的大小可以反应出不同特征对样本label的贡献度,方便我们进行特征筛选。如果不做标准化,是不能这样来筛选特征的。
6.3 标准化的注意事项
答到这里,有些厉害的面试官可能会继续问,做标准化有什么注意事项吗?
最大的注意事项就是先拆分出test集,只在训练集上标准化,即均值和标准差是从训练集中计算出来的,不要在整个数据集上做标准化,因为那样会将test集的信息引入到训练集中,造成了数据信息泄露,这是一个非常容易犯的错误。
7. 哪些模型需要标准化,哪些不需要?
7.1 需要标准化的模型

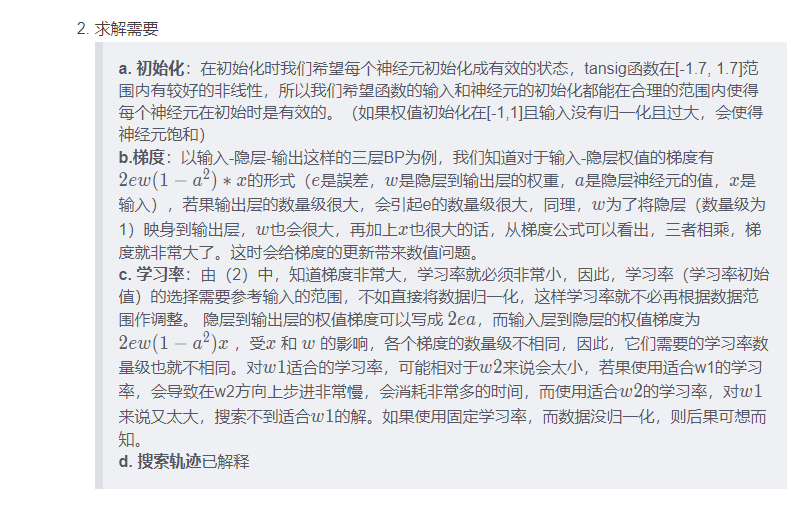

一般算法如果本身受量纲影响较大,或者相关优化函数受量纲影响大,则需要进行特征归一化。树模型特征归一化可能会降低模型的准确率,但是能够使模型更加平稳
7.2 不需要标准化的模型
当然,也不是所有的模型都需要做归一的,比如模型算法里面没有关于对距离的衡量,没有关于对变量间标准差的衡量。比如 decision tree 决策树,他采用算法里面没有涉及到任何和距离等有关的,所以在做决策树模型时,通常是不需要将变量做标准化的。
概率模型不需要归一化,因为它们不关心变量的值,而是关心变量的分布和变量之间的条件概率。
对于树形结构为什么不需要归一化?
因为数值缩放不影响分裂点位置,对树模型的结构不造成影响。
按照特征值进行排序的,排序的顺序不变,那么所属的分支以及分裂点就不会有不同。
而且,树模型是不能进行梯度下降的,因为构建树模型(回归树)寻找最优点时是通过寻找最优分裂点完成的,因此树模型是阶跃的,阶跃点是不可导的,并且求导没意义,也就不需要归一化。所以树模型(回归树)寻找最优点是通过寻找最优分裂点完成的
7.3 特殊说明
强调: 能不归一化最好不归一化,之所以进行数据归一化是因为各个维度的量纲不相同,而且需要看情况进行归一化。
有些模型在各维度进行了不均匀的伸缩之后,最优解与原来不等价(SVM)需要归一化。
有些模型伸缩与原来等价,如:LR则不用归一化,但是实际中往往通过迭代求解模型参数,如果目标函数太扁(想象一下很扁的高斯模型)迭代算法会发生不收敛的情况,所以最坏进行数据归一化。
补充:其实本质是由于loss函数不同造成的,SVM用了欧拉距离,如果一个特征很大就会把其他的维度dominated。而LR可以通过权重调整使得损失函数不变。